עקומה שומרת זווית
עקומה שומרת זווית או ספירלה לוגריתמית (באנגלית: Logarithmic Spiral או equiangular spiral) היא עקומה מיוחדת, שיוצרת בכל נקודה עם המשיק שלה את אותה זווית בדיוק. עקומות שומרות זווית מוגדרות על פי הזווית שהן שומרות. העיקרון של עקומה שומרת זווית נמצא בשימוש בכל אמצעי העיגון המבוססים על קאמים כמו פרנדים, טריקמים ואחרים. עקומות דומות נמצאות בדימוס באמצעים להתחברות לחבל כמו ברסקיו-סנדר, ברופ-מן ואמצעים אחרים.
עקומות כאלה מוכרות למתמטיקאים ולמהנדסים כבר זמן רב. השימוש הראשון במבנה כזה בטיפוס היה בשנות השלושים, כשהאלפיניסט הרוסי ויטאלי מיכאלוביץ' אבאלאקוב תכנן ובנה את העיגון הראשון שמבוסס על קאם. דרך אגב, הוא היה מהנדס ולכן אין זה מפתיע שהוא הכיר את העיקרון הכללי של עקומות שומרות זווית. לזכותו נרשמו המצאות ופיתוחים נוספים בענייני בטיחות בטיפוס. הידוע שבהם הוא האבאלאקוב, שיטת עגינה לקרח, שגם קרויה על שמו.
העקומה
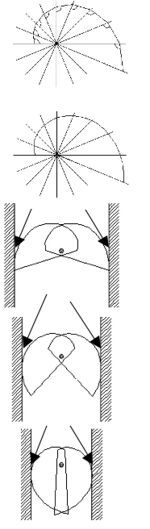
כל הקאמים בנויים כחלק מעקומה ספיראלית, כזו שתוך כדי הסיבוב שלה היא הולכת ומתרחקת מן המרכז. עקומה כזו ניתן לצייר בקלות. נקבע נקודה כלשהי כמרכז, נשרטט קרניים היוצאות ממנה במרווחי זווית קבועים, ונבחר על אחת מן הקרניים נקודת התחלה. נבחר זווית כלשהי ונתחיל לשרטט את העקומה עצמה (בציורים הזוית היא 97°). מן הקרן שנבחרה כנקודת התחלה נשרטט קטע ישר כאשר הזווית בינו לבין הקרן היא הזווית שנקבעה. בנקודה בה הקו חותך את הקרן הבאה נתחיל קטע חדש באותה הזווית הקבועה. הקו שקיבלנו בנוי מקטעים ישרים כפי שנראה בציור. הזוויות המסומנות בציור כולן שוות והן 97°. אם נקטין מאד את מרווחי הזווית בין הקרניים, ונגדיל מאד את מספר הקרניים, נקבל עקומה חלקה כפי שנראה בציור השני. בעקומה כזו הזווית בין העקומה למשיק, בכל נקודה, היא קבועה ומכאן שמה: עקומה שומרת זווית. אם הזווית בין הקרן לקו קטנה מתשעים מעלות, העקומה הולכת ומתקרבת אל המוקד. אם היא בדיוק תשעים מעלות, נקבל עיגול, כלומר המרחק אל המוקד נשאר קבוע, ואם הזווית גדולה מזווית ישרה, העקומה הולכת ומתרחקת מן המוקד.
העקומה הזו, כאמור, היא הצורה הבסיסית המשמשת לקאמים. בפרנד, למשל, הכוח מופעל לאורך קו היוצא מן המוקד (הציר של הכנפיים), ומוביל אל נקודת המגע. במקרה זה נקודת המגע היא על דופן החריץ. המבנה של הכנפיים, כעקומה שומרת זוית, גורם לכך שהזווית בין הכוח המופעל לבין משטח המגע נשארת קבועה. ניתן לראות זאת בציורים התחתונים. בציורים אלה מתואר, באופן סכמאטי, אותו הפרנד בחריצים שונים ברוחבם. קל לראות שזווית המגע עם דפנות החריץ אינה משתנה (החיצים מורים על נקודות המגע).
זווית המגע נשארת קבועה, בגלל שכך בנינו את הכנפיים, כעקומה השומרת את הזווית. זווית זו קובעת את כיוון הכוח, שקובע את החיכוך. אם הזווית נשארת שווה, גם כוח החיכוך יישאר קבוע. מכאן, שבאותו העומס יפעל אותו כוח חיכוך, ללא תלות ברוחב. פרנד, לדוגמה, מחזיק באותה המידה בחריצים קטנים וגדולים. רסקיו-סנדר מפעיל כוח דומה בשימוש בחבלים בקטרים שונים. מלבד זאת, ככל שהעומס המופעל על הקאם גדול יותר החיכוך הולך וגדל. במילים אחרות, הוא 'מחזיק' יותר טוב ככל שהכח המופעל עליו גדול יותר, זאת כמובן בתנאי שהחיכוך גדול יותר מן הכוח המופעל.
קישורים חיצוניים
תרמו לדף זה: מיכה יניב ואחרים...