רווח כוח ו־רווחי כוח: הבדלים בין דפים
יורי פלדמן (שיחה | תרומות) הפניה לדף רווחי כוח תגית: הפניה חדשה |
יורי פלדמן (שיחה | תרומות) יצירת דף עם התוכן "המונח '''רווח כוח''' או '''מערכת רווח כוח''' מתייחס לכל מערכת המאפשרת להפעיל כוח גדול על ידי שימוש במערכת תמסורת ועקרונות של יחסי העברה. מערכות כאלה ממירות כוח גדול למרחק קצר בכוח קטן למרחק גדול. בפיזיקה קלסית מוכרות מספר [http://www.lhup.edu/~dsimanek/scenario/labman1/machines.htm מכונ..." |
||
| שורה 1: | שורה 1: | ||
# | המונח '''רווח כוח''' או '''מערכת רווח כוח''' מתייחס לכל מערכת המאפשרת להפעיל כוח גדול על ידי שימוש במערכת תמסורת ועקרונות של יחסי העברה. מערכות כאלה ממירות כוח גדול למרחק קצר בכוח קטן למרחק גדול. בפיזיקה קלסית מוכרות מספר [http://www.lhup.edu/~dsimanek/scenario/labman1/machines.htm מכונות פשוטות] המבוססות על המרה כזו: מנוף, גלגלת, מישור משופע, בורג וגלגלי שיניים הן מכונות כאלה. דוגמאות מוכרות הן גלגלי שיניים ושרשראות (כמו בהילוכים של מכונית או אופנים) או רצועות (לא [[רצועות|רצועות של טיפוס]], אלא כמו במכונת כביסה או באלטרנטור של המכונית). מערכות רווח כוח נקראות לעיתים מערכות יתרון מכני (mechanical advantage). | ||
מערכות רווח כוח בעבודת חבל מבוססות על [[חבלים]] ו[[גלגלות]]. מערכות אלה משמשות בכל מקרה בו נדרש כוח גדול. מספר דוגמאות הן [[הולינג]] ב[[טיפוס מלאכותי]], מתיחה ב[[אומגה]] ומערכות חילוץ. ב[[חילוץ מוביל]], למשל, יש לעיתים צורך בהרמה. | |||
לעיתים מתבלבלים בין מערכת רווח כוח לבין [[מערכות הרמה ומתיחה|מערכת הרמה או מתיחה]]. מערכת רווח כוח הינה רק אחד החלקים במערכת הרמה, הבנויה (על פי הצורך) מרכיבים נוספים כמו [[אלחוזרים|אלחוזר]], מערכת לשחרור עומס ועוד. | |||
ולפני שמתחילים, הערה חשובה. במאמר הזה מתוארות מערכות אידיאליות, במובן זה שלצורך ההסבר והחישוב מתעלמים מן ה[[חיכוך]]. בפועל, גם בגלגלות יש חיכוך, וכאשר אין גלגלות אלא טבעות, החיכוך כלכך גדול שאם החבל עובר על שלוש טבעות או יותר - הוא מבטל את כל היתרון המכני של המערכת. בגלגלות החיכוך קטן יותר, כמובן, ואפשר לשפר את המערכת על ידי הגדלת רווח הכוח עד שימוש בכ- 8-10 גלגלות. עניין זה מוסבר בפירוט ב[[מערכות הרמה ומתיחה#חיכוך|פרק העוסק בחיכוך, במאמר על מערכות הרמה]]. | |||
=עקרונות ראשונים= | |||
כדי להבין היטב את אופי הפעולה של מערכת רווח כוח יש לזכור מספר כללים הנוגעים לכוחות הפועלים על חלקי המערכת. | |||
==סכום כוחות== | |||
סכום הכוחות על כל נקודה במערכת, אם היא נמצאת ללא תנועה, הוא אפס. כלומר, או שלא פועלים עליה כוחות כלל, או שפועלים עליה מספר כוחות המבטלים זה את זה. | |||
==מתיחות בחבל== | |||
מן הפסקה הקודמת ברור כי חבל מתוח, אם הוא אינו נע, סכום הכוחות על כל נקודה בו הוא אפס. מכיוון שעל כל נקודה בחבל פועלים שני כוחות (לאורך החבל, לשני הכיוונים), הרי שהם חייבים להיות שווים בגדלם. כוחות אלה נקראים המתיחות בחבל (באנגלית - Tension) ומסומנים ב-<math>T</math>. | |||
[[תמונה:tension.png|מרכז|ממוזער|400px|מתיחות בנקודה בחבל]] | |||
על חבל מתוח ניתן למדוד את המתיחות, והיא שווה בכל נקודה. | |||
<blockquote style="border: 1px solid blue; padding: 2em;"> | |||
*יש להבדיל בין המתיחות בחבל (tension), לבין תכונת המתיחות של החבל (אלסטיות - elasticity): | |||
<br /> | |||
tension - עד כמה החבל מתוח. יחידות המדידה הן של כוח (Kg, daN, kN). המתיחות משפיעה על ה[[חלוקת משקל|כוחות על העיגונים]], על שיטות העבודה ב[[אומגה]], ועל שיטות העבודה ב[[מערכות הרמה ומתיחה|מערכות הרמה]]. | |||
<br /> | |||
elasticity - עד כמה החבל נמתח בכוח מסויים. האלסטיות קשורה למודול של החבל. ערך זה מצויין באחוזים לכוח מתיחה מסויים. האלסטיות של החבל קובעת את ה[[חבלים#חבלים סטאטיים ודינאמיים|דינאמיות של החבל]] ומשפיעה על [[דינאמיקה של נפילות]] ו[[כוח בלימה|כוחות בלימה]]. | |||
</blockquote> | |||
==שימור אנרגיה== | |||
במערכות רווחי כוח האנרגיה היא העבודה המכנית הנעשית על מנת להזיז גוף ממקום למקום, למשל, להרים משקולת ולתת לה אנרגיה פוטנציאלית. | |||
העבודה הזו היא סכימה (אינטגרציה) של כוח לאורך דרך: | |||
<math>E_p=\int{F} d_x</math> | |||
אם הכוח קבוע למשך כל זמן הפעולה מקבלים: | |||
<math>E_p=F \cdot x</math> | |||
כמות העבודה הזו נשארת קבועה, ולכן אם מפעילים פחות כוח, הדרך מתארכת. כלומר, ניתן לבצע את אותה עבודה תוך שימוש בכוח קטן יותר, אך הדרך תגדל באותו שיעור. דוגמה שכולנו מכירים היא הכוח הנדרש לעלות בעליה תלולה וקצרה (הרבה מאמץ לאורך דרך קצרה), לעומת הכוח שדרוש לעלות בעליה ארוכה ומתונה (בלי הרבה מאמץ אבל לאורך מרחק גדול). | |||
==גלגלות== | |||
[[גלגלות|גלגלת]] היא מתקן המשנה את כיוון החבל. אם נניח שאין [[חיכוך]] בגלגלת, יהיה פשוט לחשב את הכוחות הפועלים עליה. | |||
==כוחות בגלגלות== | |||
===המתיחות בחבל העובר בגלגלת=== | |||
[[תמונה:Pulley1.png|שמאל|ממוזער|70px|חבל בגלגלת]] | |||
נבחן את החבל העובר בגלגלת. מכיוון שגלגלת רק גורמת לחבל לשנות כיוון ואינה משפיעה על המתיחות, החבל משנה את הכיוון, ועובר בגלגלת ללא הפרעה. ברור מכך, שהמתיחות לכל אורך החבל הינה שווה. כלומר, המתיחות בחבל בשני צידי הגלגלת - זהה. | |||
נראה זאת בעזרת דוגמה: אם תלויה על הגלגלת משקולת של <math>10Kg</math> (בציור - <math>W</math>), היא מפעילה על החבל כוח של <math>10Kg</math>. לכן, כדי להחזיק אותה תלויה ללא תזוזה, יהיה על האדם האוחז בחבל למשוך אותו בכוח של <math>10Kg</math> (בציור - <math>F</math>). | |||
נשים לב כי על מנת להרים את המשקולת מרחק מסויים, יש למשוך את הגלגלת מרחק זהה. על כל מטר שהגלגלת עולה, החבל המושך מתקדם במטר אחד. | |||
===הכוח על הציר של הגלגלת=== | |||
[[תמונה:Pulley2.png|שמאל|ממוזער|70px|כוחות על הגלגלת]] | |||
כעת נבחן את הכוחות הפועלים על ציר הגלגלת. את הגלגל מושכים לצד אחד שני חבלים, כל אחד במתיחות <math>T</math>. הגלגל תלוי על הציר ומפעיל עליו כוח של <math>2T</math>. מכיוון שהגלגלת אינה נעה, הרי שהעיגון מפעיל עליה כוח שווה בגדלו והפוך בכיוונו. כלומר, הכוח על העיגון עליו תלויה הגלגלת כפול מהמתיחות ושווה <math>2T</math>. | |||
ואם נשתמש באותה הדוגמה: אם תלויה על הגלגלת משקולת של <math>10Kg</math>, המתיחות בחבל היא <math>T=10Kg</math>. גם האדם האוחז בחבל מושך אותו בכוח של <math>10Kg</math>. את הגלגלת מושכים שני הכוחות הללו, ולכן, על הטבעת המחברת את הגלגלגת לעיגון (ועל העיגון עצמו), פועל כוח השווה ל <math>20Kg</math>. | |||
ובכיוון ההפוך: אם קצה החבל מחובר לעיגון, המשקולת תלויה על הגלגלת, הרי שהאדם המושך בחבל צריך למשוך רק <math>5Kg</math>, ושארית המשקל מועברת לעיגון. | |||
===יותר משני כוחות הפועלים על אותה נקודה=== | |||
[[תמונה:Pulley3.png|שמאל|ממוזער|70px|חיבור כוחות המושכים את אותו חבל]] | |||
סעיף זה מתאר נקודות במערכת עליהן פועלים כוחות נוספים מלבד המתיחות בחבל. שוב, אם כל הכוחות פועלים לאורך החבל, יהיה סכום הכוחות בכיוון אחד שווה לסכום הכוחות הפועלים בכיוון השני. | |||
לדוגמה, [[לולאת פרפר אלפיני]] באמצע החבל או [[פרוסיק]] על החבל. אם על החבל תלויה אותה משקולת, של <math>10Kg</math>, ועל קשר הפרפר תלויה משקולת נוספת, של <math>5Kg</math>, הרי שהכוח שצריך להפעיל האדם האוחז בחבל הוא משקולת של <math>10Kg+5Kg=15Kg</math>. | |||
וגם להיפך: אם את קצה החבל קשור לעיגון, את הקצה השני מחזיק אדם אחד ומושך בכוח של <math>F_1</math>, ואת הלולאה מחזיק אדם שני, ומושך בכוח של <math>F_2</math>, הרי שעל העיגון יופעל כוח של ומושך בכוח של <math>F=F_1+F_2</math>. | |||
=חישוב רווחי כוח= | |||
לניתוח מערכת נתונה וחישוב רווח הכוח נשתמש באותם שלושה כללים: | |||
'''1. המתיחות בחבל בשני צידי הגלגלת - זהה'''. | |||
'''2. הכוח על הציר של הגלגלת כפול מן המתיחות על החבל'''. | |||
'''3. אם מספר כוחות פועלים על אותה נקודה בחבל, מעבר לנקודה זו תהיה המתיחות סכום הכוחות'''. | |||
נתחיל מהחבל אותו מושכים ונסמן את הכוח שאנו מפעילים ב <math>x</math>. נתקדם לאורך החבל ונציין את הכוח בכל נקודה עד שנגיע למשקולת. היחס בין הכוחות הוא רווח הכוח של המערכת. | |||
==דוגמה 1== | |||
[[תמונה: Adv2.jpg|שמאל|ממוזער|80px|מערכת רווח כוח 2]] | |||
הכוח המופעל במשיכה הוא <math>x</math>, על הגלגלת מופעל כוח כפול מזה, ולכן, על פי כלל 2, המשקולת נמשכת בכוח של <math>2x</math>, קיבלנו מערכת רווח כוח 2. | |||
אמנם במערכת כזו נדרש חצי הכוח כדי להרים את המשקולת, אבל יש למשוך אורך חבל כפול. על כל מטר שהמשקולת עולה, יש למשוך שני מטרים של חבל. | |||
זוהי מערכת [[רווחי כוח#רווח כוח 2|רווח כוח 2]], ובשימושים מסויימים מכונה גם [[גלגלת תחתונה]]. | |||
==דוגמה 2== | |||
[[תמונה: adv3.png|שמאל|ממוזער|80px|מערכת z - רווח כוח 3]] | |||
הכוח המופעל במשיכה הוא <math>x</math>, על הגלגלת מופעל כוח כפול מזה, ולכן הפרוסיק נמשך בכוח של <math>2x</math> (כלל 2). החבל חוזר לגלגלת בעיגון ואל הפרוסיק, והמתיחות עליו היא עדיין <math>x</math>. החבל מעבר לפרוסיק נמשך על ידי הפרוסיק ב <math>2x</math> ועל ידי החבל ב <math>x</math>. כעת נפעיל את כלל 3, ונקבל כי המתיחות אחרי הפרוסיק היא <math>2x+x=3x</math>. קיבלנו מערכת רווח כוח 3. | |||
כאן נדרש רק שליש הכוח כדי להרים את המשקולת, אבל אורך החבל הדרוש כדי להרים את המשקולת הוא משולש. על כל מטר שהמשקולת עולה, יש למשוך שלושה מטרים של חבל. | |||
זוהי מערכת [[רווחי כוח#מערכת Z|מערכת Z]]. | |||
==דוגמה 3== | |||
[[תמונה: adv5.png||שמאל|ממוזער|100px|רווח כוח 5]] | |||
כמו במקרים הקודמים, הכוח המופעל במשיכה הוא <math>x</math>, על הגלגלת הראשונה מופעל כוח כפול מזה, ולכן הפרוסיק הראשון נמשך בכוח של <math>2x</math> (לפי כלל 2). החבל מעבר לפרוסיק נמשך על ידי הפרוסיק ב<math>2x</math> ועל ידי החבל ב <math>x</math>. לפי כלל 3, נקבל כי המתיחות אחרי הפרוסיק היא <math>2x+x=3x</math>.החבל חוזר לגלגלת בעיגון, והמתיחות עליו היא עדיין <math>3x</math>. גם מעבר לגלגלת יש אותה מתיחות. החבל מעבר לפרוסיק השני נמשך על ידי הפרוסיק ב <math>2x</math> ועל ידי החבל ב <math>3x</math>. נפעיל שוב את כלל 3, ונקבל כי המתיחות אחרי הפרוסיק היא <math>2x+3x=5x</math>. קיבלנו מערכת רווח כוח 5. | |||
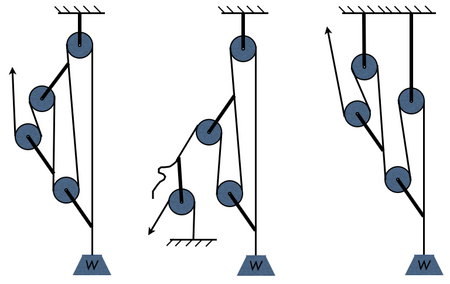
==תרגילים בחישוב רווחי כוח== | |||
לפני שנמשיך, רק כדי לוודא שהבנו, שלושה תרגילי חישוב: | |||
[[תמונה: advquiz.png|450px]] | |||
מומלץ כמובן לנסות לפתור לבד, לפני שמציצים ב[[פתרון תרגילי רווח כוח|פתרונות]]. | |||
=מערכות בסיסיות= | |||
==מערכת רווח כוח 2== | |||
מערכת רווח כוח 2 היא המערכת היעילה ביותר הקיימת, מבחינת יחס של חיכוך לרווח כוח. יש בה רק גלגלת אחת, אבל רווח כוח 2 (השוו למערכת בסעיף הבא). מצד שני - היא לא כלכך נוחה לבניה על חבל ההרמה ומצריכה חבל נפרד, וגם מיקום האלחוזר במערכת הזו אינו נוח. מצד שני, אם שמים את הגלגלת ממש על ה"משקולת" (ה[[הול-בג]] או המחולץ), מקבלים מה שנקרא [[גלגלת תחתונה]] שמכניסה רווח כוח מובנה אל תוך המערכת. מצד שלישי - זה דורש חבל ארוך פי 2. | |||
==מערכת Z== | |||
[[תמונה: zsystem.jpg|שמאל|ממוזער|300px|מערכת Z לחילוץ מ[[קרווס]]]] | |||
מערכת רווח כוח 3 נקראת גם מערכת (z pulley system) והיא נפוצה מאד. מערכת זו נפוצה ביותר בשימוש ב[[אלפיניזם]] ובמערכות [[חילוץ]]. נוח להשתמש בה כי היא יעילה, מהירה לבניה, ומאפשרת לשים [[אלחוזרים|אלחוזר]] במקום נוח, ואינטואיטיבי (על אותו החבל) ומאחורי המערכת. | |||
מערכת זו מתאימה למרבית המצבים: עזרה למטפס שני, הרמה בחילוץ, חילוץ מ[[קרווס|קרווסים]] ובהרים, [[הולינג]] ועוד. | |||
==גלגלת תחתונה== | |||
זהו שם למערכת רווח כוח 2, כאשר הגלגלת נמצאת על המשקולת ממש (ולא מחוברת אל החבל המגיע מן המשקולת). בדרך כלל מורידים גלגלת או את אמצע החבל אל המחולץ, והוא מתחבר אליה (מכאן השם באנגלית: drop loop haul system). | |||
=עקרונות מתקדמים= | |||
ניתן ליצור רווחי כוח מורכבים מן המערכות הפשוטות שתוארו בפרקים הקודמים. לשם הבהירות, נסכם כי נתחיל לרשום את רווח הכוח מהחבל המושך ונתקדם לכיוון המשקולת. | |||
==חיבור רווחי כוח== | |||
בחיבור רווחי כוח מוסיפים מערכות פשוטות שכולן מושכות את המשקולת. על ידי שימוש באותו החבל שוב ושוב ניתן להגדיל את רווח הכוח. כל תוספת של גלגלת בעיגון וגלגלת במשקולת תגדיל את רווח הכוח ב-2. | |||
לדוגמה: רווח כוח 2, רווח כוח 4, רווח כוח 6. | |||
[[תמונה: adv_add_even.png|450px]] | |||
שיטה זו, של חיבור רווחי כוח, נקראת [[אשכול גלגלות]] (באנגלית: pulley block). מקור הכינוי במערכות מוכנות שבהן מספר רב של גלגלות מובנות על ציר משותף (block and tackle). מבנה סכמטי של מערכת כזו דומה למערכת של רווח כוח 6 בדוגמה. | |||
ועוד דוגמה: רווח כוח 1, רווח כוח 3, רווח כוח 5. | |||
[[תמונה: adv_add_odd.png|450px]] | |||
מערכת Z (רווח כוח 3) היא דוגמה טובה לזה. מערכת זו היא למעשה רווח כוח שמחברת <math>2+1</math>. | |||
==הכפלת רווחי כוח== | |||
[[תמונה: adv_mult1.png|left|100px]] | |||
הרעיון כאן הוא לבנות מערכת רווח כוח שנייה שתמשוך את החבל היוצא מן הראשונה (ולא את המשקולת עצמה). ננסה להבין זאת בשלבים. בתרשים הראשון המשקולת <math>W</math>. נמשכת במערכת רווח כוח פשוטה (במקרה זה - רווח כוח 3). החבל היוצא מן המערכת מרגיש רק שליש מן המשקל. נכניס את כל המערכת לקופסה (בדמיון), כולל העיגון והמשקולת, זוהי המסגרת המקווקוות. יש לנו עכשיו חבל (זה שיוצא מן המסגרת) המחובר למשקולת של שליש המשקולת המקורית או <math>w/3</math>. | |||
נתייחס אליו כאילו הוא המשקולת ונמשוך אותו ברווח כוח נוסף, במקרה זה - רווח כוח 2. קיבלנו מערכת רווח כוח <math>2\times3</math>. | |||
למעשה, מיקום העיגון והמשקולת האמיתיים אינו חשוב. אפשר להתעלם מכל המערכת הראשונה, ולהתייחס רק לחבל היוצא ממנה. אפשר להוציא את העיגון והמשקולת מן ה"קופסה". | |||
[[תמונה: adv_mult2.png|left|200px]] | |||
בתרשים הבא מוצגות שתי מערכות רווח כוח 6, אחת שכבר ראינו: | |||
<math>2\times3</math> | |||
והשניה בהיפוך סדר המערכות: | |||
<math>3\times2</math> | |||
==כיוון המשיכה והכוח על העיגון== | |||
[[תמונה: adv_sub1.png|left|120px]] | |||
בתרשים משמאל משורטטת מערכת קצת הזויה, נניח כי זוהי מערכת רווח כוח <math>k</math>. מכיוון שהקופסה, המסגרת בה נמצאת המערכת אינה זזה, הרי שלפי אחד הכללים שלנו, סכום הכוחות על עליה הוא אפס. כלומר, או שלא פועלים עליה כוחות כלל, או שפועלים עליה מספר כוחות המבטלים זה את זה. | |||
על הקופסה פועלים שלשה כוחות: | |||
החבל המושך: <math>F_1</math> אותו סימנו ב <math>x</math>. | |||
החבל המחובר לעיגון: <math>F_2</math> | |||
החבל המחובר למשקולת: <math>W</math> | |||
ידוע לנו היחס בין <math>F_1</math> ו <math>W</math>. זהו רווח הכוח, ולכן: | |||
<math>W=k\times x</math> | |||
מכאן, קל לחשב את הכוח על העיגון <math>F_2</math>: | |||
<math>F_2=W-F_1=k\times x-x=(k-1)\times x</math> | |||
[[תמונה: adv_sub2.png|left|120px]] | |||
אם נהפוך את כיון המשיכה בעזרת גלגלת בעיגון, לא נשנה את רווח הכוח, אבל נגדיל את הכוח על העיגון ב <math>2x</math>: | |||
<math>F_2=W+2F_1=(k-1)\times x+2F_1=(k-1)\times x+2x=(k+1)\times x</math> | |||
בכל מקרה, הערך המוחלט של ההפרש בין הכוח על המשקולת לבין הכוח על העיגון הוא <math>x</math> וסימנו מתחלף עם כיוון המשיכה. | |||
==רווחי כוח זוגיים ואי-זוגיים== | |||
ניתן לקבל רווחי כוח זוגיים או איזוגיים בחיבור, בכפל, או בשילוב של שניהם. לאחר שהבנו את המבנה היוצר חיבור וכפל, הבנייה היא על פי הפעולות האלגבריות הפשוטות. | |||
===חיבור של רווחי כוח=== | |||
אם מתחילים מגלגלת תחתונה ומחברים רווחי כוח, מקבלים רווחי כוח זוגיים, כאשר כל זוג גלגלות (בעיגון ובמשקולת) מגדיל את רווח הכוח ב-2. | |||
אם מתחילים מהחבל הקשור למשקולת (רווח כוח 1) ומחברים רווחי כוח, מקבלים רווחי כוח איזוגיים, כאשר, שוב, כל זוג גלגלות מגדיל את רווח הכוח ב-2. | |||
===כפל של רווחי כוח=== | |||
כפל של כל מספר ב- 2 ייתן מספר זוגי, מכאן שאם יש במערכת רווח כוח 2, בקונפיגורציה של כפל, המערכת כולה תהיה זוגית. | |||
ברור, לכן, ששימוש בגלגלת תחתונה, למשל, עם כל הכפלה נוספת של רווח כוח, ייתן תמיד רווח כוח זוגי. | |||
כדי לקבל רווח כוח איזוגי בהכפלת רווחי כוח, עלינו לכפול רווחי כוח איזוגיים בלבד, למשל: | |||
<math>3^2=3\times3=9</math> | |||
או: | |||
<math>3^3=3\times3\times3 =27</math> | |||
או: | |||
<math>3 \times5=15</math> | |||
==עוד כמה תרגילים== | |||
בנה את המערכות המתאימות למבנה הבא: | |||
<math>2^3</math> | |||
<math>3^2</math> | |||
רווח כוח 4 בשתי צורות (<math>2+2</math>; <math>2*2</math>) | |||
רווח כוח 9 בשתי צורות | |||
=ענייינים מעשיים= | |||
==גלגלות בעולם האמיתי== | |||
כל החישובים והשרטוטים של רווחי כוח, מניחים שהגלגלות הן אידיאליות, כלומר - שאין [[חיכוך]] בגלגלות. למעשה, יש חיכוך בכל גלגלת, גם בטובה ביותר. בעצם, ההנחה היא שיש לחבל יותר חיכוך עם הגלגל של הגלגלת, מאשר יש לגלגלת עם הציר שלה. במקרה כזה, החבל לא ינוע ביחס לגלגל בכלל, ורק הגלגל ינוע ביחס לציר, וייקח איתו את החבל. זה נכון בכל גלגלת, מלבד הגרועות ביותר. למשל, ב[[גלגלת פלאסטיק|גלגלות פלאסטיק]] פשוטות, כאלה שמקליפים על טבעת אובאלית, אפשר לראות שילוב של שתי התנועות האלה, כי גם החבל מחליק על הגלגלת, וגם הגלגלת מסתובבת על הטבעת. זו גלגלת לא כלכך טובה, כמובן, אבל לעומת זאת היא קלה מאד. | |||
===מיסבי החלקה=== | |||
מיסבי החלקה הם פשוט שלוש טבעות: החיצונית עם מקדם חיכוך גדול עם החבל (כך שהחבל לא יחליק עליה), הפנימית עם מקדם חיכוך גדול עם הציר (כך שהיא תסתובב עם הציר ולא תחליק עליו), והאמצעית - עם מקדם חיכוך קטן מאד עם שתי האחרות. הטבעת האמצעית עשויה הדרך כלל מחומר פלסטי קשיח (כמו אוקולון, למשל) או מחומר שמפריש חומרי סיכה במהלך השימוש. למיסבים כאלה תוחלת חיים לא ארוכה. | |||
מיסבים כאלה, למשל, נמצאים בגלגלת של ה[[revolver]], של DMM. | |||
===מיסבי גלגול=== | |||
מיסבי גלגול הם שתי טבעות מחומר קשה מאד, שביניהם כדורים או גלילים (או לפעמים - קונוסים) מפלדה קשה. הרעיון הוא שכשמסובבים את הטבעת החיצונית, אין החלקה בכלל כי הכדורים לשתי הטבעות, כי הכדורים בעצמם מתגלגלים ולא מחליקים. במיסב כדורים טוב אפשר להקטין את החיכוך באופן משמעותי. בגלגלות טובות מאד (ויקרות למדי) משתמשים במיסבים כאלה. | |||
==כמה חיכוך יש בגלגלת?== | |||
שני הדברים שמשפיעים על החיכוך בגלגלת הם: | |||
# קוטר הגלגל: מתחת לקוטר מסויים, יש יותר סיכוי להחלקה של החבל על הגלגל. זה מוריד את היעילות של השימוש בגלגלת. תופעה זו נובעת מכך שלחבל יש רדיוס עקמומיות מינימאלי, שתלוי ב[[נוטביליטי]] שלו, כמובן. בחבלי [[ליבה ומעטפת]] של טיפוס, גלישה וחילוץ, הגודל הזה הוא בערך פי 5 מקוטר החבל כלומר - כ-50מ"מ. בגלגלות עם גלגלים בקוטר קטן נוצר, הלכה למעשה, [[ניפ]] בחבל. המשמעות היא שעומס גדול נופל על חלק מן הסיבים בחבל והם עלולים להיקרע. עם הגלגול, הניפ הזה עובר לאורך החבל ועשוי ליצור פגיעה קטנה לכל אורך החבל. במילים אחרות, גלגל קטן מאד גם מקצר את חיי החבל. מקובל כי הגודל הקריטי לעניין זה הוא פי 3 מקוטר החבל. | |||
# איכות המיסבים: למיסבי החלקה, כאמור, יש יותר חיכוך ממיסבי גלגול. במיסבי גלגול יש מספר רמות של איכות, שתלויה במספר הכדורים (שאומר משהו על ה[[מאמץ ומעוות|מעוות]] שהמיסב מקבל תחת עומס), בקושי של החומר ממנו עשויים הכדורים (כלומר: כמה הם נמעכים תחת עומס) ובדיוק של הטבעות. | |||
כמות החיכוך בגלגלת ניתנת על ידי היצרן, ומסומנת ביחס בין המתיחות בחבל בשני צידי הגלגלת. אם למשל, מצויין, שיעילות של גלגלת מסויימת היא 80%, המשמעות היא שרק 80% מהמתיחות, עוברת לצד השני של הגלגלת. כלומר, אם מושכים ב-100ק"ג בצד אחד של הגלגלגת, אפשר להרים רק 80ק"ג. | |||
לחברת Petzl יש שלושה דגמים של גלגלות נפוצות: | |||
[[תמונה: P50_pulley.jpg|שמאל|ממוזער|50px|P50]] | |||
לדגם הנפוץ של גלגלות של Petzl, ה-P50, יש יעילות של 95%. | |||
[[תמונה: mini_pulley.jpg|שמאל|ממוזער|50px|Mini]] | |||
לדגם הקצת יותר קטן, גם הוא עם מיסבי כדורים טובים, ה-Mini, יש יעילות של 91%. | |||
[[תמונה: fixe_pulley.jpg|שמאל|ממוזער|50px|fixe]] | |||
לדגם הקטן והעוד יותר פשוט, עם מיסבי החלקה, ה-FIXE, יש יעילות של 71%. | |||
===תוספת החיכוך=== | |||
אפשר לראות שהחיכוך לא מתווסף מגלגלת לגלגלת, אלא מכפיל את עצמו. כלומר, אם יעילות של גלגלת היא <math>80%</math>, יעילות של מערכת עם שתי גלגלות היא <math>80%^2</math> כלומר <math>64%</math>. | |||
==גלגלות או טבעות== | |||
לחבל שעובר על טבעת יש חיכוך קצת יותר מלחבל שעובר על תוף. אופן החישוב מוסבר בפירוט במאמר על [[איך עובדים אמצעי חיכוך?]] ולא נחזור עליו כאן. בכל אופן, יעילות טיפוסית היא כ-2/3, כלומר, שרק חצי מכל הכוח שיש בצד אחד, עובר לצד השני. אנחנו מכירים את זה מ[[אבטחה]] ב[[טופ-רופ]], כשמאבטח קל יכול לאבטח מישהו הרבה יותר כבד. | |||
במערכות רווח כוח, טבעות דופקות את העניין לגמרי. כל זמן שיש שתיים או שלוש טבעות, עדיין רווח הכוח גדל, בארבע טבעות ומעלה, כבר אין גידול ברווח הכוח בכלל, וההפסדים על חיכוך גדולים יותר מהגידול בכוח. | |||
בטבלה הבאה מוצגים הערכים המתאימים לכוח המתקבל (במכפלות של כוח המשיכה) במספר מערכות רווחי כוח, בשלושה מקרים: עם גלגלות P50 (יעילות של 95%), עם גלגלות Mini (יעילות של 91%) ועם טבעות (יעילות של 66%). | |||
{| border="1" | |||
|רווח כוח תיאורטי||מספר גלגלות||מבנה מערכת||רווח כוח אמיתי עם גלגלות P50 (יעילות 0.95)||רווח כוח אמיתי עם גלגלות Mini (יעילות 0.91)||רווח כוח אמיתי עם טבעות (יעילות 0.66) | |||
|- | |||
|2||1||גלגלת תחתונה ||1.95||1.91||1.66 | |||
|- | |||
|3||2||מערכת z||2.85||2.74||2.10 | |||
|- | |||
|4||2||2*2||3.80||3.65||2.76 | |||
|- | |||
|4||3||2+2||3.71||3.49||2.38 | |||
|- | |||
|5||3||3+2||4.52||4.18||2.57 | |||
|- | |||
|6||3||3*2||5.56||5.23||3.48 | |||
|- | |||
|6||5||2+2+2||5.30||4.80||2.70 | |||
|- | |||
|8||3||2*2*2||6.51||6.14||4.14 | |||
|- | |||
|8||7||2+2+2+2||6.73||5.89||2.84 | |||
|- | |||
|9||4||3*3||8.14||7.58||4.62 | |||
|} | |||
=קישורים חיצוניים= | |||
* [http://www.hawills.com/pulleys.htm חומר מעשי על גלגלות] | |||
* [http://www.the-office.com/summerlift/pulleybasics.htm הסבר בסיסי על גלגלות ניידות ונייחות] | |||
---- | |||
תרמו לדף זה: [[משתמש: מיכה יניב|מיכה יניב]] ואחרים... | |||
[[קטגוריה: טכניקות ומיומנויות]][[קטגוריה: חילוץ]][[קטגוריה: מאמרים מתורגמים ומקוריים]] | |||
גרסה אחרונה מ־23:32, 4 בדצמבר 2024
המונח רווח כוח או מערכת רווח כוח מתייחס לכל מערכת המאפשרת להפעיל כוח גדול על ידי שימוש במערכת תמסורת ועקרונות של יחסי העברה. מערכות כאלה ממירות כוח גדול למרחק קצר בכוח קטן למרחק גדול. בפיזיקה קלסית מוכרות מספר מכונות פשוטות המבוססות על המרה כזו: מנוף, גלגלת, מישור משופע, בורג וגלגלי שיניים הן מכונות כאלה. דוגמאות מוכרות הן גלגלי שיניים ושרשראות (כמו בהילוכים של מכונית או אופנים) או רצועות (לא רצועות של טיפוס, אלא כמו במכונת כביסה או באלטרנטור של המכונית). מערכות רווח כוח נקראות לעיתים מערכות יתרון מכני (mechanical advantage).
מערכות רווח כוח בעבודת חבל מבוססות על חבלים וגלגלות. מערכות אלה משמשות בכל מקרה בו נדרש כוח גדול. מספר דוגמאות הן הולינג בטיפוס מלאכותי, מתיחה באומגה ומערכות חילוץ. בחילוץ מוביל, למשל, יש לעיתים צורך בהרמה.
לעיתים מתבלבלים בין מערכת רווח כוח לבין מערכת הרמה או מתיחה. מערכת רווח כוח הינה רק אחד החלקים במערכת הרמה, הבנויה (על פי הצורך) מרכיבים נוספים כמו אלחוזר, מערכת לשחרור עומס ועוד.
ולפני שמתחילים, הערה חשובה. במאמר הזה מתוארות מערכות אידיאליות, במובן זה שלצורך ההסבר והחישוב מתעלמים מן החיכוך. בפועל, גם בגלגלות יש חיכוך, וכאשר אין גלגלות אלא טבעות, החיכוך כלכך גדול שאם החבל עובר על שלוש טבעות או יותר - הוא מבטל את כל היתרון המכני של המערכת. בגלגלות החיכוך קטן יותר, כמובן, ואפשר לשפר את המערכת על ידי הגדלת רווח הכוח עד שימוש בכ- 8-10 גלגלות. עניין זה מוסבר בפירוט בפרק העוסק בחיכוך, במאמר על מערכות הרמה.
עקרונות ראשונים
כדי להבין היטב את אופי הפעולה של מערכת רווח כוח יש לזכור מספר כללים הנוגעים לכוחות הפועלים על חלקי המערכת.
סכום כוחות
סכום הכוחות על כל נקודה במערכת, אם היא נמצאת ללא תנועה, הוא אפס. כלומר, או שלא פועלים עליה כוחות כלל, או שפועלים עליה מספר כוחות המבטלים זה את זה.
מתיחות בחבל
מן הפסקה הקודמת ברור כי חבל מתוח, אם הוא אינו נע, סכום הכוחות על כל נקודה בו הוא אפס. מכיוון שעל כל נקודה בחבל פועלים שני כוחות (לאורך החבל, לשני הכיוונים), הרי שהם חייבים להיות שווים בגדלם. כוחות אלה נקראים המתיחות בחבל (באנגלית - Tension) ומסומנים ב-[math]\displaystyle{ T }[/math].
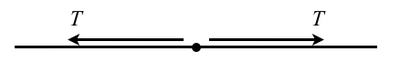
על חבל מתוח ניתן למדוד את המתיחות, והיא שווה בכל נקודה.
- יש להבדיל בין המתיחות בחבל (tension), לבין תכונת המתיחות של החבל (אלסטיות - elasticity):
tension - עד כמה החבל מתוח. יחידות המדידה הן של כוח (Kg, daN, kN). המתיחות משפיעה על הכוחות על העיגונים, על שיטות העבודה באומגה, ועל שיטות העבודה במערכות הרמה.
elasticity - עד כמה החבל נמתח בכוח מסויים. האלסטיות קשורה למודול של החבל. ערך זה מצויין באחוזים לכוח מתיחה מסויים. האלסטיות של החבל קובעת את הדינאמיות של החבל ומשפיעה על דינאמיקה של נפילות וכוחות בלימה.
שימור אנרגיה
במערכות רווחי כוח האנרגיה היא העבודה המכנית הנעשית על מנת להזיז גוף ממקום למקום, למשל, להרים משקולת ולתת לה אנרגיה פוטנציאלית. העבודה הזו היא סכימה (אינטגרציה) של כוח לאורך דרך:
[math]\displaystyle{ E_p=\int{F} d_x }[/math]
אם הכוח קבוע למשך כל זמן הפעולה מקבלים:
[math]\displaystyle{ E_p=F \cdot x }[/math]
כמות העבודה הזו נשארת קבועה, ולכן אם מפעילים פחות כוח, הדרך מתארכת. כלומר, ניתן לבצע את אותה עבודה תוך שימוש בכוח קטן יותר, אך הדרך תגדל באותו שיעור. דוגמה שכולנו מכירים היא הכוח הנדרש לעלות בעליה תלולה וקצרה (הרבה מאמץ לאורך דרך קצרה), לעומת הכוח שדרוש לעלות בעליה ארוכה ומתונה (בלי הרבה מאמץ אבל לאורך מרחק גדול).
גלגלות
גלגלת היא מתקן המשנה את כיוון החבל. אם נניח שאין חיכוך בגלגלת, יהיה פשוט לחשב את הכוחות הפועלים עליה.
כוחות בגלגלות
המתיחות בחבל העובר בגלגלת
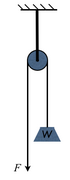
נבחן את החבל העובר בגלגלת. מכיוון שגלגלת רק גורמת לחבל לשנות כיוון ואינה משפיעה על המתיחות, החבל משנה את הכיוון, ועובר בגלגלת ללא הפרעה. ברור מכך, שהמתיחות לכל אורך החבל הינה שווה. כלומר, המתיחות בחבל בשני צידי הגלגלת - זהה.
נראה זאת בעזרת דוגמה: אם תלויה על הגלגלת משקולת של [math]\displaystyle{ 10Kg }[/math] (בציור - [math]\displaystyle{ W }[/math]), היא מפעילה על החבל כוח של [math]\displaystyle{ 10Kg }[/math]. לכן, כדי להחזיק אותה תלויה ללא תזוזה, יהיה על האדם האוחז בחבל למשוך אותו בכוח של [math]\displaystyle{ 10Kg }[/math] (בציור - [math]\displaystyle{ F }[/math]).
נשים לב כי על מנת להרים את המשקולת מרחק מסויים, יש למשוך את הגלגלת מרחק זהה. על כל מטר שהגלגלת עולה, החבל המושך מתקדם במטר אחד.
הכוח על הציר של הגלגלת
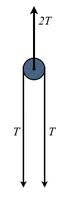
כעת נבחן את הכוחות הפועלים על ציר הגלגלת. את הגלגל מושכים לצד אחד שני חבלים, כל אחד במתיחות [math]\displaystyle{ T }[/math]. הגלגל תלוי על הציר ומפעיל עליו כוח של [math]\displaystyle{ 2T }[/math]. מכיוון שהגלגלת אינה נעה, הרי שהעיגון מפעיל עליה כוח שווה בגדלו והפוך בכיוונו. כלומר, הכוח על העיגון עליו תלויה הגלגלת כפול מהמתיחות ושווה [math]\displaystyle{ 2T }[/math].
ואם נשתמש באותה הדוגמה: אם תלויה על הגלגלת משקולת של [math]\displaystyle{ 10Kg }[/math], המתיחות בחבל היא [math]\displaystyle{ T=10Kg }[/math]. גם האדם האוחז בחבל מושך אותו בכוח של [math]\displaystyle{ 10Kg }[/math]. את הגלגלת מושכים שני הכוחות הללו, ולכן, על הטבעת המחברת את הגלגלגת לעיגון (ועל העיגון עצמו), פועל כוח השווה ל [math]\displaystyle{ 20Kg }[/math].
ובכיוון ההפוך: אם קצה החבל מחובר לעיגון, המשקולת תלויה על הגלגלת, הרי שהאדם המושך בחבל צריך למשוך רק [math]\displaystyle{ 5Kg }[/math], ושארית המשקל מועברת לעיגון.
יותר משני כוחות הפועלים על אותה נקודה
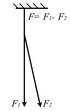
סעיף זה מתאר נקודות במערכת עליהן פועלים כוחות נוספים מלבד המתיחות בחבל. שוב, אם כל הכוחות פועלים לאורך החבל, יהיה סכום הכוחות בכיוון אחד שווה לסכום הכוחות הפועלים בכיוון השני.
לדוגמה, לולאת פרפר אלפיני באמצע החבל או פרוסיק על החבל. אם על החבל תלויה אותה משקולת, של [math]\displaystyle{ 10Kg }[/math], ועל קשר הפרפר תלויה משקולת נוספת, של [math]\displaystyle{ 5Kg }[/math], הרי שהכוח שצריך להפעיל האדם האוחז בחבל הוא משקולת של [math]\displaystyle{ 10Kg+5Kg=15Kg }[/math].
וגם להיפך: אם את קצה החבל קשור לעיגון, את הקצה השני מחזיק אדם אחד ומושך בכוח של [math]\displaystyle{ F_1 }[/math], ואת הלולאה מחזיק אדם שני, ומושך בכוח של [math]\displaystyle{ F_2 }[/math], הרי שעל העיגון יופעל כוח של ומושך בכוח של [math]\displaystyle{ F=F_1+F_2 }[/math].
חישוב רווחי כוח
לניתוח מערכת נתונה וחישוב רווח הכוח נשתמש באותם שלושה כללים:
1. המתיחות בחבל בשני צידי הגלגלת - זהה.
2. הכוח על הציר של הגלגלת כפול מן המתיחות על החבל.
3. אם מספר כוחות פועלים על אותה נקודה בחבל, מעבר לנקודה זו תהיה המתיחות סכום הכוחות.
נתחיל מהחבל אותו מושכים ונסמן את הכוח שאנו מפעילים ב [math]\displaystyle{ x }[/math]. נתקדם לאורך החבל ונציין את הכוח בכל נקודה עד שנגיע למשקולת. היחס בין הכוחות הוא רווח הכוח של המערכת.
דוגמה 1
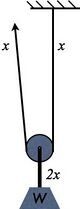
הכוח המופעל במשיכה הוא [math]\displaystyle{ x }[/math], על הגלגלת מופעל כוח כפול מזה, ולכן, על פי כלל 2, המשקולת נמשכת בכוח של [math]\displaystyle{ 2x }[/math], קיבלנו מערכת רווח כוח 2.
אמנם במערכת כזו נדרש חצי הכוח כדי להרים את המשקולת, אבל יש למשוך אורך חבל כפול. על כל מטר שהמשקולת עולה, יש למשוך שני מטרים של חבל.
זוהי מערכת רווח כוח 2, ובשימושים מסויימים מכונה גם גלגלת תחתונה.
דוגמה 2
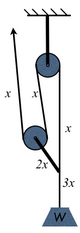
הכוח המופעל במשיכה הוא [math]\displaystyle{ x }[/math], על הגלגלת מופעל כוח כפול מזה, ולכן הפרוסיק נמשך בכוח של [math]\displaystyle{ 2x }[/math] (כלל 2). החבל חוזר לגלגלת בעיגון ואל הפרוסיק, והמתיחות עליו היא עדיין [math]\displaystyle{ x }[/math]. החבל מעבר לפרוסיק נמשך על ידי הפרוסיק ב [math]\displaystyle{ 2x }[/math] ועל ידי החבל ב [math]\displaystyle{ x }[/math]. כעת נפעיל את כלל 3, ונקבל כי המתיחות אחרי הפרוסיק היא [math]\displaystyle{ 2x+x=3x }[/math]. קיבלנו מערכת רווח כוח 3.
כאן נדרש רק שליש הכוח כדי להרים את המשקולת, אבל אורך החבל הדרוש כדי להרים את המשקולת הוא משולש. על כל מטר שהמשקולת עולה, יש למשוך שלושה מטרים של חבל.
זוהי מערכת מערכת Z.
דוגמה 3
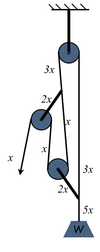
כמו במקרים הקודמים, הכוח המופעל במשיכה הוא [math]\displaystyle{ x }[/math], על הגלגלת הראשונה מופעל כוח כפול מזה, ולכן הפרוסיק הראשון נמשך בכוח של [math]\displaystyle{ 2x }[/math] (לפי כלל 2). החבל מעבר לפרוסיק נמשך על ידי הפרוסיק ב[math]\displaystyle{ 2x }[/math] ועל ידי החבל ב [math]\displaystyle{ x }[/math]. לפי כלל 3, נקבל כי המתיחות אחרי הפרוסיק היא [math]\displaystyle{ 2x+x=3x }[/math].החבל חוזר לגלגלת בעיגון, והמתיחות עליו היא עדיין [math]\displaystyle{ 3x }[/math]. גם מעבר לגלגלת יש אותה מתיחות. החבל מעבר לפרוסיק השני נמשך על ידי הפרוסיק ב [math]\displaystyle{ 2x }[/math] ועל ידי החבל ב [math]\displaystyle{ 3x }[/math]. נפעיל שוב את כלל 3, ונקבל כי המתיחות אחרי הפרוסיק היא [math]\displaystyle{ 2x+3x=5x }[/math]. קיבלנו מערכת רווח כוח 5.
תרגילים בחישוב רווחי כוח
לפני שנמשיך, רק כדי לוודא שהבנו, שלושה תרגילי חישוב:
מומלץ כמובן לנסות לפתור לבד, לפני שמציצים בפתרונות.
מערכות בסיסיות
מערכת רווח כוח 2
מערכת רווח כוח 2 היא המערכת היעילה ביותר הקיימת, מבחינת יחס של חיכוך לרווח כוח. יש בה רק גלגלת אחת, אבל רווח כוח 2 (השוו למערכת בסעיף הבא). מצד שני - היא לא כלכך נוחה לבניה על חבל ההרמה ומצריכה חבל נפרד, וגם מיקום האלחוזר במערכת הזו אינו נוח. מצד שני, אם שמים את הגלגלת ממש על ה"משקולת" (ההול-בג או המחולץ), מקבלים מה שנקרא גלגלת תחתונה שמכניסה רווח כוח מובנה אל תוך המערכת. מצד שלישי - זה דורש חבל ארוך פי 2.
מערכת Z
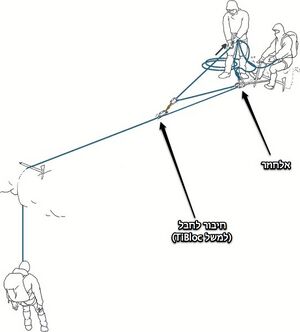
מערכת רווח כוח 3 נקראת גם מערכת (z pulley system) והיא נפוצה מאד. מערכת זו נפוצה ביותר בשימוש באלפיניזם ובמערכות חילוץ. נוח להשתמש בה כי היא יעילה, מהירה לבניה, ומאפשרת לשים אלחוזר במקום נוח, ואינטואיטיבי (על אותו החבל) ומאחורי המערכת.
מערכת זו מתאימה למרבית המצבים: עזרה למטפס שני, הרמה בחילוץ, חילוץ מקרווסים ובהרים, הולינג ועוד.
גלגלת תחתונה
זהו שם למערכת רווח כוח 2, כאשר הגלגלת נמצאת על המשקולת ממש (ולא מחוברת אל החבל המגיע מן המשקולת). בדרך כלל מורידים גלגלת או את אמצע החבל אל המחולץ, והוא מתחבר אליה (מכאן השם באנגלית: drop loop haul system).
עקרונות מתקדמים
ניתן ליצור רווחי כוח מורכבים מן המערכות הפשוטות שתוארו בפרקים הקודמים. לשם הבהירות, נסכם כי נתחיל לרשום את רווח הכוח מהחבל המושך ונתקדם לכיוון המשקולת.
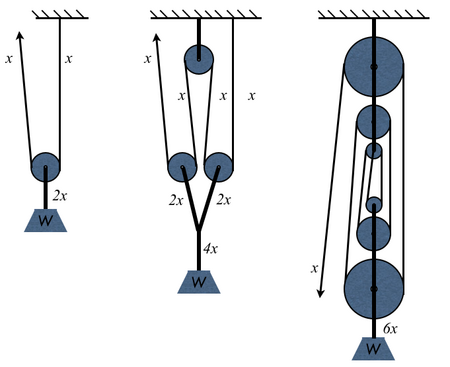
חיבור רווחי כוח
בחיבור רווחי כוח מוסיפים מערכות פשוטות שכולן מושכות את המשקולת. על ידי שימוש באותו החבל שוב ושוב ניתן להגדיל את רווח הכוח. כל תוספת של גלגלת בעיגון וגלגלת במשקולת תגדיל את רווח הכוח ב-2.
לדוגמה: רווח כוח 2, רווח כוח 4, רווח כוח 6.
שיטה זו, של חיבור רווחי כוח, נקראת אשכול גלגלות (באנגלית: pulley block). מקור הכינוי במערכות מוכנות שבהן מספר רב של גלגלות מובנות על ציר משותף (block and tackle). מבנה סכמטי של מערכת כזו דומה למערכת של רווח כוח 6 בדוגמה.
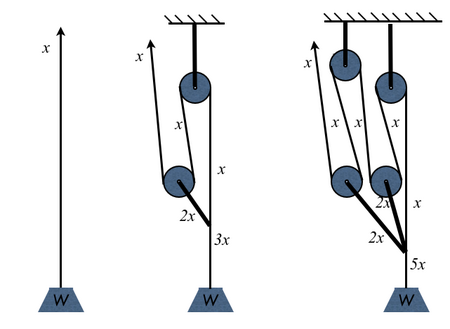
ועוד דוגמה: רווח כוח 1, רווח כוח 3, רווח כוח 5.
מערכת Z (רווח כוח 3) היא דוגמה טובה לזה. מערכת זו היא למעשה רווח כוח שמחברת [math]\displaystyle{ 2+1 }[/math].
הכפלת רווחי כוח
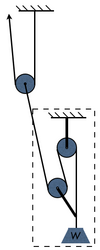
הרעיון כאן הוא לבנות מערכת רווח כוח שנייה שתמשוך את החבל היוצא מן הראשונה (ולא את המשקולת עצמה). ננסה להבין זאת בשלבים. בתרשים הראשון המשקולת [math]\displaystyle{ W }[/math]. נמשכת במערכת רווח כוח פשוטה (במקרה זה - רווח כוח 3). החבל היוצא מן המערכת מרגיש רק שליש מן המשקל. נכניס את כל המערכת לקופסה (בדמיון), כולל העיגון והמשקולת, זוהי המסגרת המקווקוות. יש לנו עכשיו חבל (זה שיוצא מן המסגרת) המחובר למשקולת של שליש המשקולת המקורית או [math]\displaystyle{ w/3 }[/math].
נתייחס אליו כאילו הוא המשקולת ונמשוך אותו ברווח כוח נוסף, במקרה זה - רווח כוח 2. קיבלנו מערכת רווח כוח [math]\displaystyle{ 2\times3 }[/math].
למעשה, מיקום העיגון והמשקולת האמיתיים אינו חשוב. אפשר להתעלם מכל המערכת הראשונה, ולהתייחס רק לחבל היוצא ממנה. אפשר להוציא את העיגון והמשקולת מן ה"קופסה".
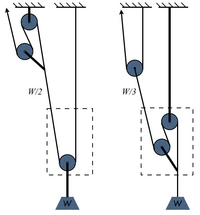
בתרשים הבא מוצגות שתי מערכות רווח כוח 6, אחת שכבר ראינו:
[math]\displaystyle{ 2\times3 }[/math]
והשניה בהיפוך סדר המערכות:
[math]\displaystyle{ 3\times2 }[/math]
כיוון המשיכה והכוח על העיגון
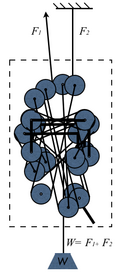
בתרשים משמאל משורטטת מערכת קצת הזויה, נניח כי זוהי מערכת רווח כוח [math]\displaystyle{ k }[/math]. מכיוון שהקופסה, המסגרת בה נמצאת המערכת אינה זזה, הרי שלפי אחד הכללים שלנו, סכום הכוחות על עליה הוא אפס. כלומר, או שלא פועלים עליה כוחות כלל, או שפועלים עליה מספר כוחות המבטלים זה את זה.
על הקופסה פועלים שלשה כוחות:
החבל המושך: [math]\displaystyle{ F_1 }[/math] אותו סימנו ב [math]\displaystyle{ x }[/math].
החבל המחובר לעיגון: [math]\displaystyle{ F_2 }[/math]
החבל המחובר למשקולת: [math]\displaystyle{ W }[/math]
ידוע לנו היחס בין [math]\displaystyle{ F_1 }[/math] ו [math]\displaystyle{ W }[/math]. זהו רווח הכוח, ולכן:
[math]\displaystyle{ W=k\times x }[/math]
מכאן, קל לחשב את הכוח על העיגון [math]\displaystyle{ F_2 }[/math]:
[math]\displaystyle{ F_2=W-F_1=k\times x-x=(k-1)\times x }[/math]
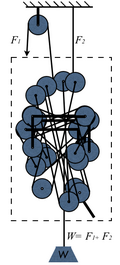
אם נהפוך את כיון המשיכה בעזרת גלגלת בעיגון, לא נשנה את רווח הכוח, אבל נגדיל את הכוח על העיגון ב [math]\displaystyle{ 2x }[/math]:
[math]\displaystyle{ F_2=W+2F_1=(k-1)\times x+2F_1=(k-1)\times x+2x=(k+1)\times x }[/math]
בכל מקרה, הערך המוחלט של ההפרש בין הכוח על המשקולת לבין הכוח על העיגון הוא [math]\displaystyle{ x }[/math] וסימנו מתחלף עם כיוון המשיכה.
רווחי כוח זוגיים ואי-זוגיים
ניתן לקבל רווחי כוח זוגיים או איזוגיים בחיבור, בכפל, או בשילוב של שניהם. לאחר שהבנו את המבנה היוצר חיבור וכפל, הבנייה היא על פי הפעולות האלגבריות הפשוטות.
חיבור של רווחי כוח
אם מתחילים מגלגלת תחתונה ומחברים רווחי כוח, מקבלים רווחי כוח זוגיים, כאשר כל זוג גלגלות (בעיגון ובמשקולת) מגדיל את רווח הכוח ב-2.
אם מתחילים מהחבל הקשור למשקולת (רווח כוח 1) ומחברים רווחי כוח, מקבלים רווחי כוח איזוגיים, כאשר, שוב, כל זוג גלגלות מגדיל את רווח הכוח ב-2.
כפל של רווחי כוח
כפל של כל מספר ב- 2 ייתן מספר זוגי, מכאן שאם יש במערכת רווח כוח 2, בקונפיגורציה של כפל, המערכת כולה תהיה זוגית.
ברור, לכן, ששימוש בגלגלת תחתונה, למשל, עם כל הכפלה נוספת של רווח כוח, ייתן תמיד רווח כוח זוגי.
כדי לקבל רווח כוח איזוגי בהכפלת רווחי כוח, עלינו לכפול רווחי כוח איזוגיים בלבד, למשל:
[math]\displaystyle{ 3^2=3\times3=9 }[/math]
או:
[math]\displaystyle{ 3^3=3\times3\times3 =27 }[/math]
או:
[math]\displaystyle{ 3 \times5=15 }[/math]
עוד כמה תרגילים
בנה את המערכות המתאימות למבנה הבא:
[math]\displaystyle{ 2^3 }[/math]
[math]\displaystyle{ 3^2 }[/math]
רווח כוח 4 בשתי צורות ([math]\displaystyle{ 2+2 }[/math]; [math]\displaystyle{ 2*2 }[/math])
רווח כוח 9 בשתי צורות
ענייינים מעשיים
גלגלות בעולם האמיתי
כל החישובים והשרטוטים של רווחי כוח, מניחים שהגלגלות הן אידיאליות, כלומר - שאין חיכוך בגלגלות. למעשה, יש חיכוך בכל גלגלת, גם בטובה ביותר. בעצם, ההנחה היא שיש לחבל יותר חיכוך עם הגלגל של הגלגלת, מאשר יש לגלגלת עם הציר שלה. במקרה כזה, החבל לא ינוע ביחס לגלגל בכלל, ורק הגלגל ינוע ביחס לציר, וייקח איתו את החבל. זה נכון בכל גלגלת, מלבד הגרועות ביותר. למשל, בגלגלות פלאסטיק פשוטות, כאלה שמקליפים על טבעת אובאלית, אפשר לראות שילוב של שתי התנועות האלה, כי גם החבל מחליק על הגלגלת, וגם הגלגלת מסתובבת על הטבעת. זו גלגלת לא כלכך טובה, כמובן, אבל לעומת זאת היא קלה מאד.
מיסבי החלקה
מיסבי החלקה הם פשוט שלוש טבעות: החיצונית עם מקדם חיכוך גדול עם החבל (כך שהחבל לא יחליק עליה), הפנימית עם מקדם חיכוך גדול עם הציר (כך שהיא תסתובב עם הציר ולא תחליק עליו), והאמצעית - עם מקדם חיכוך קטן מאד עם שתי האחרות. הטבעת האמצעית עשויה הדרך כלל מחומר פלסטי קשיח (כמו אוקולון, למשל) או מחומר שמפריש חומרי סיכה במהלך השימוש. למיסבים כאלה תוחלת חיים לא ארוכה.
מיסבים כאלה, למשל, נמצאים בגלגלת של הrevolver, של DMM.
מיסבי גלגול
מיסבי גלגול הם שתי טבעות מחומר קשה מאד, שביניהם כדורים או גלילים (או לפעמים - קונוסים) מפלדה קשה. הרעיון הוא שכשמסובבים את הטבעת החיצונית, אין החלקה בכלל כי הכדורים לשתי הטבעות, כי הכדורים בעצמם מתגלגלים ולא מחליקים. במיסב כדורים טוב אפשר להקטין את החיכוך באופן משמעותי. בגלגלות טובות מאד (ויקרות למדי) משתמשים במיסבים כאלה.
כמה חיכוך יש בגלגלת?
שני הדברים שמשפיעים על החיכוך בגלגלת הם:
- קוטר הגלגל: מתחת לקוטר מסויים, יש יותר סיכוי להחלקה של החבל על הגלגל. זה מוריד את היעילות של השימוש בגלגלת. תופעה זו נובעת מכך שלחבל יש רדיוס עקמומיות מינימאלי, שתלוי בנוטביליטי שלו, כמובן. בחבלי ליבה ומעטפת של טיפוס, גלישה וחילוץ, הגודל הזה הוא בערך פי 5 מקוטר החבל כלומר - כ-50מ"מ. בגלגלות עם גלגלים בקוטר קטן נוצר, הלכה למעשה, ניפ בחבל. המשמעות היא שעומס גדול נופל על חלק מן הסיבים בחבל והם עלולים להיקרע. עם הגלגול, הניפ הזה עובר לאורך החבל ועשוי ליצור פגיעה קטנה לכל אורך החבל. במילים אחרות, גלגל קטן מאד גם מקצר את חיי החבל. מקובל כי הגודל הקריטי לעניין זה הוא פי 3 מקוטר החבל.
- איכות המיסבים: למיסבי החלקה, כאמור, יש יותר חיכוך ממיסבי גלגול. במיסבי גלגול יש מספר רמות של איכות, שתלויה במספר הכדורים (שאומר משהו על המעוות שהמיסב מקבל תחת עומס), בקושי של החומר ממנו עשויים הכדורים (כלומר: כמה הם נמעכים תחת עומס) ובדיוק של הטבעות.
כמות החיכוך בגלגלת ניתנת על ידי היצרן, ומסומנת ביחס בין המתיחות בחבל בשני צידי הגלגלת. אם למשל, מצויין, שיעילות של גלגלת מסויימת היא 80%, המשמעות היא שרק 80% מהמתיחות, עוברת לצד השני של הגלגלת. כלומר, אם מושכים ב-100ק"ג בצד אחד של הגלגלגת, אפשר להרים רק 80ק"ג.
לחברת Petzl יש שלושה דגמים של גלגלות נפוצות:

לדגם הנפוץ של גלגלות של Petzl, ה-P50, יש יעילות של 95%.

לדגם הקצת יותר קטן, גם הוא עם מיסבי כדורים טובים, ה-Mini, יש יעילות של 91%.

לדגם הקטן והעוד יותר פשוט, עם מיסבי החלקה, ה-FIXE, יש יעילות של 71%.
תוספת החיכוך
אפשר לראות שהחיכוך לא מתווסף מגלגלת לגלגלת, אלא מכפיל את עצמו. כלומר, אם יעילות של גלגלת היא [math]\displaystyle{ 80% }[/math], יעילות של מערכת עם שתי גלגלות היא [math]\displaystyle{ 80%^2 }[/math] כלומר [math]\displaystyle{ 64% }[/math].
גלגלות או טבעות
לחבל שעובר על טבעת יש חיכוך קצת יותר מלחבל שעובר על תוף. אופן החישוב מוסבר בפירוט במאמר על איך עובדים אמצעי חיכוך? ולא נחזור עליו כאן. בכל אופן, יעילות טיפוסית היא כ-2/3, כלומר, שרק חצי מכל הכוח שיש בצד אחד, עובר לצד השני. אנחנו מכירים את זה מאבטחה בטופ-רופ, כשמאבטח קל יכול לאבטח מישהו הרבה יותר כבד.
במערכות רווח כוח, טבעות דופקות את העניין לגמרי. כל זמן שיש שתיים או שלוש טבעות, עדיין רווח הכוח גדל, בארבע טבעות ומעלה, כבר אין גידול ברווח הכוח בכלל, וההפסדים על חיכוך גדולים יותר מהגידול בכוח.
בטבלה הבאה מוצגים הערכים המתאימים לכוח המתקבל (במכפלות של כוח המשיכה) במספר מערכות רווחי כוח, בשלושה מקרים: עם גלגלות P50 (יעילות של 95%), עם גלגלות Mini (יעילות של 91%) ועם טבעות (יעילות של 66%).
| רווח כוח תיאורטי | מספר גלגלות | מבנה מערכת | רווח כוח אמיתי עם גלגלות P50 (יעילות 0.95) | רווח כוח אמיתי עם גלגלות Mini (יעילות 0.91) | רווח כוח אמיתי עם טבעות (יעילות 0.66) |
| 2 | 1 | גלגלת תחתונה | 1.95 | 1.91 | 1.66 |
| 3 | 2 | מערכת z | 2.85 | 2.74 | 2.10 |
| 4 | 2 | 2*2 | 3.80 | 3.65 | 2.76 |
| 4 | 3 | 2+2 | 3.71 | 3.49 | 2.38 |
| 5 | 3 | 3+2 | 4.52 | 4.18 | 2.57 |
| 6 | 3 | 3*2 | 5.56 | 5.23 | 3.48 |
| 6 | 5 | 2+2+2 | 5.30 | 4.80 | 2.70 |
| 8 | 3 | 2*2*2 | 6.51 | 6.14 | 4.14 |
| 8 | 7 | 2+2+2+2 | 6.73 | 5.89 | 2.84 |
| 9 | 4 | 3*3 | 8.14 | 7.58 | 4.62 |
קישורים חיצוניים
תרמו לדף זה: מיכה יניב ואחרים...