הבדלים בין גרסאות בדף "כוחות בבלימת נפילה"
| (20 גרסאות ביניים של 2 משתמשים אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
| − | מאמר זה מנסה להסביר איך לחשב את ה'''כוחות המתפתחים | + | מאמר זה מנסה להסביר איך לחשב את ה'''כוחות המתפתחים בזמן בלימה''' של נפילת [[הובלה|מוביל]], בתנאים אידיאליים. |
==הנחות עבודה== | ==הנחות עבודה== | ||
| − | *אין חיכוך של | + | * אין [[חיכוך]] של ה[[חבלים|חבל]] בשום גורם אחר. |
| − | + | * ה[[איבטוח]] סטאטי ולא [[אבטחה דינאמית|דינאמי]] (אין החלקת חבל ב[[אמצעי חיכוך|אביזר החיכוך]]). | |
| − | * | + | * החבל מעוגן ב[[עגינות|עיגון]] קבוע בצד ה[[אבטוח]]. |
| − | |||
| − | *החבל מעוגן | ||
| − | |||
==סימונים== | ==סימונים== | ||
<math>L</math> – אורך החבל (1 Ft רגל=0.3מטר). | <math>L</math> – אורך החבל (1 Ft רגל=0.3מטר). | ||
| שורה 18: | שורה 15: | ||
<math>K</math> – קשיחות החבל (מוגדרת ע"י קבוע החבל ואורך החבל בו מדובר). | <math>K</math> – קשיחות החבל (מוגדרת ע"י קבוע החבל ואורך החבל בו מדובר). | ||
| − | <math>M</math> – מודול החבל (לכל חבל מודול משלו). | + | <math>M</math> – [[מודול]] החבל (לכל חבל מודול משלו). |
<math>\delta</math> - השינוי באורך החבל. | <math>\delta</math> - השינוי באורך החבל. | ||
| שורה 46: | שורה 43: | ||
<math>F=kX</math> (כאשר <math>k</math> - קבוע הקפיץ, <math>X</math> -השינוי באורך הקפיץ). | <math>F=kX</math> (כאשר <math>k</math> - קבוע הקפיץ, <math>X</math> -השינוי באורך הקפיץ). | ||
| − | חבל, בניגוד לקפיץ, אינו מקיים יחס קבוע בין הכוח למידת ההתארכות שלו. את החבל קל יותר למתוח מקפיץ כאשר הוא רפוי, וקשה יותר כאשר הוא מתוח. לכן, ההנחה ש<math>K</math> של החבל הינו לינארי היא הנחה מחמירה, שכן האנרגיה | + | חבל, בניגוד לקפיץ, אינו מקיים יחס קבוע בין הכוח למידת ההתארכות שלו. את החבל קל יותר למתוח מקפיץ כאשר הוא רפוי, וקשה יותר כאשר הוא מתוח. לכן, ההנחה ש-<math>K</math> של החבל הינו לינארי היא הנחה מחמירה, שכן האנרגיה הנספגת בקפיץ גבוהה יותר מזו שנספגת בחבל (השטח מתחת לקו הישר גדול מזה שמתחת לעקומה). ואז נקבל כי: |
<math>F(x)=K\delta</math> | <math>F(x)=K\delta</math> | ||
| שורה 72: | שורה 69: | ||
<math>F=W\left(1+\sqrt{1+\frac{2M}{W}FF}\right)</math> | <math>F=W\left(1+\sqrt{1+\frac{2M}{W}FF}\right)</math> | ||
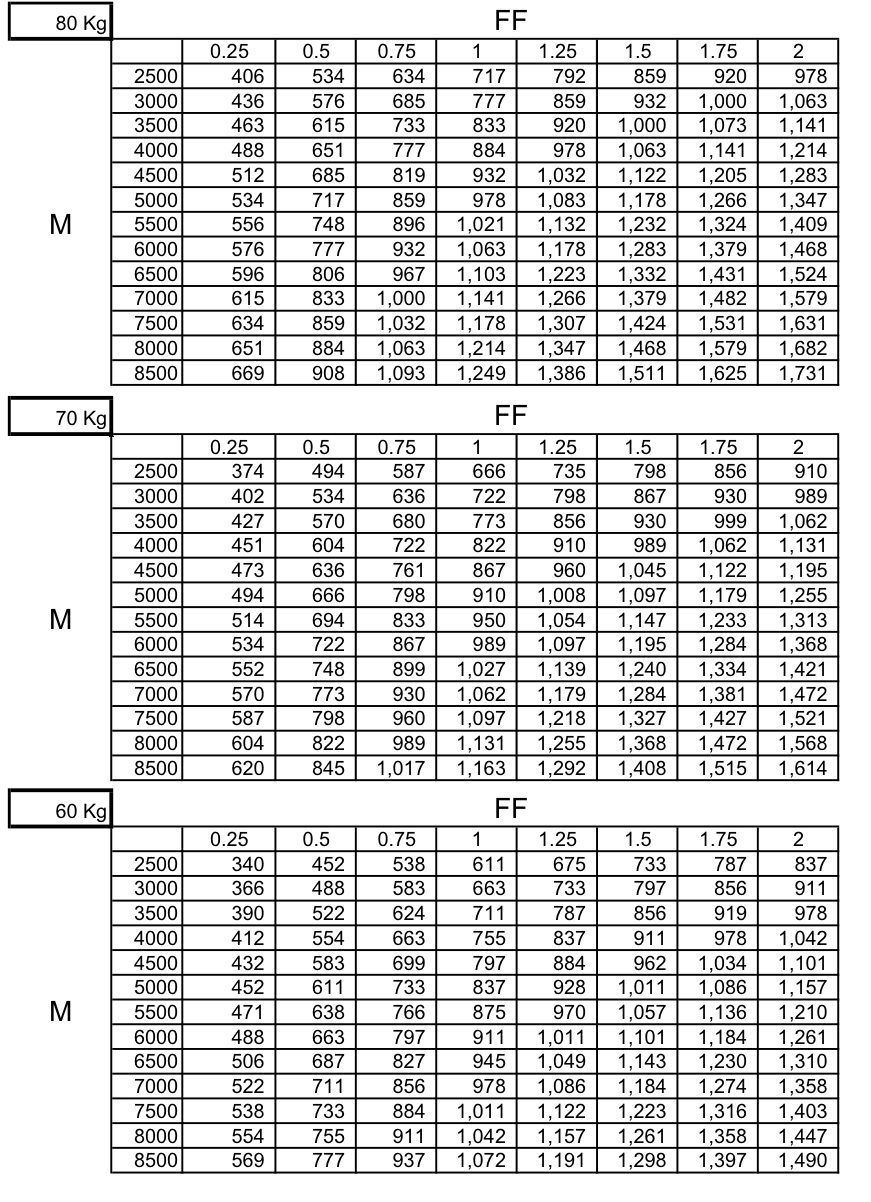
| − | טבלאות | + | כעת ניתן לחשב את הכוח המקסימאלי לערכים שונים של <math>M</math> ,<math>W</math> ,<math>FF</math>. מובאות כאן שלוש טבלאות כאלה (התוצאות ביחידות קג"כ): |
| − | [[תמונה:IF table.jpg]] | + | [[תמונה:IF table.jpg|600px]] |
קביעת מודול החבל מתוך נתוני היצרן: | קביעת מודול החבל מתוך נתוני היצרן: | ||
| − | היצרן מספק לנו בד"כ נתונים עבור נפילה סטנדרטית: | + | היצרן מספק לנו בד"כ נתונים עבור [[נפילת UIAA|נפילה סטנדרטית]]: |
<math>F=1.78</math> | <math>F=1.78</math> | ||
| שורה 99: | שורה 96: | ||
<math>M=22.5\times\left(\left(\frac{900}{80}-1\right)^2 -1\right)=2340kg</math> | <math>M=22.5\times\left(\left(\frac{900}{80}-1\right)^2 -1\right)=2340kg</math> | ||
| − | מודולים של חבלי הובלה הם באזור <math>2500 kg | + | מודולים של חבלי הובלה הם באזור <math>2500 kg/sec^2</math> ושל חבלים סטטיים באזור <math>8500 kg/sec^2</math>. |
=מרחקים בין עיגונים בהובלה= | =מרחקים בין עיגונים בהובלה= | ||
| שורה 106: | שורה 103: | ||
לבדיקה זו נחלק את העיגונים לשני סוגים: | לבדיקה זו נחלק את העיגונים לשני סוגים: | ||
| − | עיגונים בעלי חוזק גבוה (למשל בולטים אשר מותקנים היטב, הקסים על סלינג וכו' ) כ– 1800ק"ג | + | עיגונים בעלי חוזק גבוה (למשל בולטים אשר מותקנים היטב, הקסים על סלינג וכו') כ– 1800ק"ג. |
| + | |||
| + | עיגונים בעלי חוזק נמוך (למשל רוקים ו - camming devices) כ- 900ק"ג. | ||
| − | |||
מאחר ואנו מניחים כי העומס על העיגון האחרון כפול מהעומס על המטפס, נרצה כי העומס על המטפס לא יעלה על 900 ו 450 ק"ג בהתאמה. | מאחר ואנו מניחים כי העומס על העיגון האחרון כפול מהעומס על המטפס, נרצה כי העומס על המטפס לא יעלה על 900 ו 450 ק"ג בהתאמה. | ||
דוגמאות חישוב: | דוגמאות חישוב: | ||
| שורה 114: | שורה 112: | ||
===עיגון בעל חוזק גבוה=== | ===עיגון בעל חוזק גבוה=== | ||
עומס מותר על המטפס 900 ק"ג,
| עומס מותר על המטפס 900 ק"ג,
| ||
| − | לכן בהנחה שמטפס שוקל 80 ק"ג FF המותר הוא בערך 1-1.25.
| + | לכן בהנחה שמטפס שוקל 80 ק"ג <math>FF</math> המותר הוא בערך 1-1.25.
|
מכאן שמותר לטפס מעל העיגון קצת פחות ממרחק העיגון מעל האבטוח (יש לקחת בחשבון מתיחות אם לא רוצים להימרח על הקרקע). | מכאן שמותר לטפס מעל העיגון קצת פחות ממרחק העיגון מעל האבטוח (יש לקחת בחשבון מתיחות אם לא רוצים להימרח על הקרקע). | ||
===עיגון בעל חוזק נמוך=== | ===עיגון בעל חוזק נמוך=== | ||
עומס מותר על המטפס 450 ק"ג,
| עומס מותר על המטפס 450 ק"ג,
| ||
| − | לכן בהנחה שמטפס שוקל 80 ק"ג FF המותר הוא בערך 0.25-0.3.
| + | לכן בהנחה שמטפס שוקל 80 ק"ג <math>FF</math> המותר הוא בערך 0.25-0.3.
|
מכאן שמותר לטפס מעל העיגון קצת פחות משישית מגובהו של העיגון מעל האבטוח (שוב, יש לקחת בחשבון מתיחות אם לא רוצים להימרח על הקרקע). | מכאן שמותר לטפס מעל העיגון קצת פחות משישית מגובהו של העיגון מעל האבטוח (שוב, יש לקחת בחשבון מתיחות אם לא רוצים להימרח על הקרקע). | ||
| שורה 166: | שורה 164: | ||
|} | |} | ||
| − | מהטבלה ניתן לראות בקלות כי יש להתחשב גם בגובה הנפילה בלי קשר ל- FF מאחר ובמהירויות גבוהות פגיעה בסלע (אם הנפילה אינה באוויר) עלולה להיות בלתי נעימה ואף מסוכנת. | + | מהטבלה ניתן לראות בקלות כי יש להתחשב גם בגובה הנפילה בלי קשר ל- <math>FF</math> מאחר ובמהירויות גבוהות פגיעה בסלע (אם הנפילה אינה באוויר) עלולה להיות בלתי נעימה ואף מסוכנת. |
==נושאים נוספים== | ==נושאים נוספים== | ||
| − | + | ניתן לתאר את השפעתם של אופי האבטחה וחיכוך ב[[טבעות]] (במיוחד בטבעת העליונה, של העיגון האחרון) ובסלע, על הכוחות המתפתחים בזמן בלימת נפילה. החלקת החבל באביזר החיכוך והתרוממות המאבטח משפיעים גם הם, בכך שהם מגדילים את מרחק הבלימה. נושאים אלה הינם מחוץ לתחומה של עבודה זו וההתייחסות אליהם היא ערכית ולא מספרית. | |
==אופי האבטחה== | ==אופי האבטחה== | ||
אופי האבטחה (דינאמית או סטאטית) משפיע על כוח הבלימה. [[אבטחה דינאמית]] מגדילה את מרחק הבלימה, וכוח הבלימה קטן בהתאם. | אופי האבטחה (דינאמית או סטאטית) משפיע על כוח הבלימה. [[אבטחה דינאמית]] מגדילה את מרחק הבלימה, וכוח הבלימה קטן בהתאם. | ||
| שורה 177: | שורה 175: | ||
גם החלקת החבל דרך אביזר החיכוך תורמת להקטנת חומרת הנפילה. בזמן החלקת החבל באביזר החיכוך מתבצעת עבודה באביזר החיכוך (כמו גם בחלקי המערכת האחרים), בהערכה גסה, אם נניח שמחליק כחצי מטר דרך אביזר החיכוך, וכוח הבלימה הוא כ150 קג' כוח, הרי שהחלקה כזו שוות ערך להקטנת אורך הנפילה בכ1 מטר. | גם החלקת החבל דרך אביזר החיכוך תורמת להקטנת חומרת הנפילה. בזמן החלקת החבל באביזר החיכוך מתבצעת עבודה באביזר החיכוך (כמו גם בחלקי המערכת האחרים), בהערכה גסה, אם נניח שמחליק כחצי מטר דרך אביזר החיכוך, וכוח הבלימה הוא כ150 קג' כוח, הרי שהחלקה כזו שוות ערך להקטנת אורך הנפילה בכ1 מטר. | ||
==חיכוך== | ==חיכוך== | ||
| − | חיכוך בטבעות ממיר חלק של האנרגיה | + | חיכוך בטבעות ממיר חלק של האנרגיה לחום. מתבצעת עבודה אשר יש לקחת בחשבון בחישובי האנרגיה. ה[[מקדם נפילה אפקטיבי|חיכוך בטבעת העליונה]] משפיע במיוחד על הכוחות מאחר והוא "מפריד" בין החבל הקשור למטפס ובין החבל ההולך לאמצעי החיכוך. קל להבין זאת אם נדמיין טבעת בעלת חיכוך אינסופי, שהחבל אינו זורם בה כלל. במקרה כזה, יימתח רק החבל מצד אחד של הטבעת, זה שמופעל עליו הכוח - זה שעליו תלוי המוביל. הכוח הפועל על המטפס שנפל יגדל, והכוח הפועל על המאבטח יקטן (במידה גדולה יותר מאשר הגדלת הכוח על המטפס). |
ניתן לחשב מחדש את הכוחות לקבלת הערכה טובה יותר (וגם זו רק הערכה). | ניתן לחשב מחדש את הכוחות לקבלת הערכה טובה יותר (וגם זו רק הערכה). | ||
החישובים בעבודה זו מבוססים על [http://www.amrg.org/Rope_system_analysis_Attaway.pdf עבודתו של Stephen W. Attaway] שכתב לזכרם של שלושה חברים אשר נהרגו בנפילה של 259 מטר ב23 ביוני 1996 (סיפור המקרה הופיע במגזין Climbing). | החישובים בעבודה זו מבוססים על [http://www.amrg.org/Rope_system_analysis_Attaway.pdf עבודתו של Stephen W. Attaway] שכתב לזכרם של שלושה חברים אשר נהרגו בנפילה של 259 מטר ב23 ביוני 1996 (סיפור המקרה הופיע במגזין Climbing). | ||
| + | ==קריאה נוספת== | ||
| + | * [[שיטות הובלה]] | ||
| + | * [[מקדם נפילה]] | ||
| + | * [[מקדם נפילה אפקטיבי]] | ||
| + | * [[כוח בלימה]] | ||
| + | * [[אבטחה דינאמית]] | ||
| + | * [[אבטחה דינאמית למתקדמים]] | ||
| + | ==קישורים חיצוניים== | ||
| + | * [http://personal.strath.ac.uk/andrew.mclaren/Pavier.pdf כוחות בזמן בלימת נפילה] | ||
---- | ---- | ||
| − | תרמו לדף זה: מיכה יניב, דורון נצר, ארנון נצר ואחרים... | + | תרמו לדף זה: [[משתמש: מיכה יניב|מיכה יניב]], דורון נצר, ארנון נצר ואחרים... |
| + | |||
| + | [[קטגוריה: טכניקות ומיומנויות]][[קטגוריה: טיפוס הרים]][[קטגוריה:טיפוס סלע]][[קטגוריה: טיפוס מלאכותי]][[קטגוריה: טיפוס]][[קטגוריה: מאמרים מתורגמים ומקוריים]][[קטגוריה: בטיחות]] | ||
גרסה אחרונה מ־02:55, 23 ביוני 2014
מאמר זה מנסה להסביר איך לחשב את הכוחות המתפתחים בזמן בלימה של נפילת מוביל, בתנאים אידיאליים.
תוכן עניינים
הנחות עבודה
- אין חיכוך של החבל בשום גורם אחר.
- האיבטוח סטאטי ולא דינאמי (אין החלקת חבל באביזר החיכוך).
- החבל מעוגן בעיגון קבוע בצד האבטוח.
סימונים
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): L – אורך החבל (1 Ft רגל=0.3מטר).
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): W – משקל המטפס (LBS 1 ליברה =0.45ק"ג).
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): FF - מקדם הנפילה.
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): F - כוח הבלימה - הכוח המקסימאלי על המוביל בנפילה.
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): K – קשיחות החבל (מוגדרת ע"י קבוע החבל ואורך החבל בו מדובר).
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): M – מודול החבל (לכל חבל מודול משלו).
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \delta - השינוי באורך החבל.
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \epsilon - היחס בין אורכו המקורי של החבל והשינוי באורכו.
היחסים הבאים מתקיימים:
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): K=\frac{M}{L}
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): M=\frac{F}{\epsilon}
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \epsilon=\frac{L}{\delta}
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \delta=\frac{F}{K}
הנחה: עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): M קבוע ואינו משתנה תחת עומס.
האנרגיה הפוטנציאלית של המטפס:
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): E_P=mg\left(h+\delta\right)=W\left(h+\delta\right)
את כל החישובים נערוך תחת ההנחה שהחבל מתנהג בדומה לקפיץ. בקפיץ מתקיים יחס קבוע בין הכוח המותח אותו לבין מידת ההתארכות: עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): F=kX (כאשר עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): k - קבוע הקפיץ, עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): X -השינוי באורך הקפיץ).
חבל, בניגוד לקפיץ, אינו מקיים יחס קבוע בין הכוח למידת ההתארכות שלו. את החבל קל יותר למתוח מקפיץ כאשר הוא רפוי, וקשה יותר כאשר הוא מתוח. לכן, ההנחה ש-עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): K של החבל הינו לינארי היא הנחה מחמירה, שכן האנרגיה הנספגת בקפיץ גבוהה יותר מזו שנספגת בחבל (השטח מתחת לקו הישר גדול מזה שמתחת לעקומה). ואז נקבל כי:
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): F(x)=K\delta
האנרגיה הנאגרת בקפיץ הסופג את הנפילה (החבל):
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): E=\int_0^\delta F(x)dx=\frac{k\delta^2}{2}
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): E_P=E
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): W(h+\delta)=\frac{k\delta^2}{2}
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \frac{k\delta^2}{2}-w\delta-Wh=0
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \delta=\frac{W\pm\sqrt{W^2+2WKh}}{K}=\frac{W\pm W\sqrt{1+\frac{2Kh}{W}}}{K}=\frac{W\pm W\sqrt{1+\frac{2Mh}{WL}}}{K}
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): F=K\delta=W\left(1\pm\sqrt{1+\frac{2Mh}{WL}}\right)
ניתן להתייחס רק לשורש החיובי של המשוואה מאחר ולשורש השלילי נקבל ערך שלילי למשוואה כולה, ומקבלים כי הכוח המקסימאלי על המוביל הוא:
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): F=W\left(1+\sqrt{1+\frac{2Mh}{WL}}\right)
הכוח מקסימאלי על המוביל כפונקציה של המודול, משקל המטפס ומקדם הנפילה הוא :
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): F=W\left(1+\sqrt{1+\frac{2M}{W}FF}\right)
כעת ניתן לחשב את הכוח המקסימאלי לערכים שונים של עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): M ,עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): W ,עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): FF . מובאות כאן שלוש טבלאות כאלה (התוצאות ביחידות קג"כ):
קביעת מודול החבל מתוך נתוני היצרן:
היצרן מספק לנו בד"כ נתונים עבור נפילה סטנדרטית:
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): F=1.78
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): W=80Kg
F – הכוח המקסימאלי שיפעל בנפילה כזאת על המטפס:
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): M=\frac{W}{2FF}\left(\left(\frac{F}{W}-1^2\right) -1\right)
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): M=\frac{80kg}{2\times1.78}\left(\left(\frac{F}{80kg}-1\right)^2 -1\right)=22.5\times\left(\left(\frac{F}{80}-1\right)^2 -1\right)
לדוגמא: אם היצרן מצהיר על 80 KN כוח מקסימאלי אז M יהיה:
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): M=22.5\times\left(\left(\frac{800}{80}-1\right)^2 -1\right)=1800kg
אם היצרן מצהיר על 90 KN כוח מקסימאלי אז M יהיה :
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): M=22.5\times\left(\left(\frac{900}{80}-1\right)^2 -1\right)=2340kg
מודולים של חבלי הובלה הם באזור עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): 2500 kg/sec^2 ושל חבלים סטטיים באזור עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): 8500 kg/sec^2 .
מרחקים בין עיגונים בהובלה
חלק זה ינסה לבדוק מהו הגובה הבטוח מעל העיגון האחרון אליו ניתן לטפס ללא הנחת עיגון נוסף.
לבדיקה זו נחלק את העיגונים לשני סוגים:
עיגונים בעלי חוזק גבוה (למשל בולטים אשר מותקנים היטב, הקסים על סלינג וכו') כ– 1800ק"ג.
עיגונים בעלי חוזק נמוך (למשל רוקים ו - camming devices) כ- 900ק"ג.
מאחר ואנו מניחים כי העומס על העיגון האחרון כפול מהעומס על המטפס, נרצה כי העומס על המטפס לא יעלה על 900 ו 450 ק"ג בהתאמה. דוגמאות חישוב:
עיגון בעל חוזק גבוה
עומס מותר על המטפס 900 ק"ג, לכן בהנחה שמטפס שוקל 80 ק"ג עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): FF המותר הוא בערך 1-1.25. מכאן שמותר לטפס מעל העיגון קצת פחות ממרחק העיגון מעל האבטוח (יש לקחת בחשבון מתיחות אם לא רוצים להימרח על הקרקע).
עיגון בעל חוזק נמוך
עומס מותר על המטפס 450 ק"ג, לכן בהנחה שמטפס שוקל 80 ק"ג עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): FF המותר הוא בערך 0.25-0.3. מכאן שמותר לטפס מעל העיגון קצת פחות משישית מגובהו של העיגון מעל האבטוח (שוב, יש לקחת בחשבון מתיחות אם לא רוצים להימרח על הקרקע).
מהירות הנופל ברגע התחלת הבלימה
נשתמש בנוסחה לחישוב נפילה חופשית:
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): V_t^2-V_0^2=2gh
מאחר והמהירות ההתחלתית היא 0 ו- עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): g=9.8 נקבל כי:
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): V_t^2=19.6h m/sec
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): V_t=4.43\sqrt{h}h m/sec
| עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): V_t [Km/Hr] | עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): h [m] |
| 16 | 1 |
| 23 | 2 |
| 32 | 4 |
| 39 | 6 |
| 45 | 8 |
| 50 | 10 |
| 55 | 12 |
| 60 | 14 |
| 64 | 16 |
| 68 | 18 |
| 71 | 20 |
| 75 | 22 |
| 78 | 24 |
מהטבלה ניתן לראות בקלות כי יש להתחשב גם בגובה הנפילה בלי קשר ל- עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): FF מאחר ובמהירויות גבוהות פגיעה בסלע (אם הנפילה אינה באוויר) עלולה להיות בלתי נעימה ואף מסוכנת.
נושאים נוספים
ניתן לתאר את השפעתם של אופי האבטחה וחיכוך בטבעות (במיוחד בטבעת העליונה, של העיגון האחרון) ובסלע, על הכוחות המתפתחים בזמן בלימת נפילה. החלקת החבל באביזר החיכוך והתרוממות המאבטח משפיעים גם הם, בכך שהם מגדילים את מרחק הבלימה. נושאים אלה הינם מחוץ לתחומה של עבודה זו וההתייחסות אליהם היא ערכית ולא מספרית.
אופי האבטחה
אופי האבטחה (דינאמית או סטאטית) משפיע על כוח הבלימה. אבטחה דינאמית מגדילה את מרחק הבלימה, וכוח הבלימה קטן בהתאם.
תנועת המאבטח גם היא מורידה מהעומס על המערכת. כאשר המאבטח מתרומם כלפי מעלה בזמן עצירת הנפילה, הרי שהוא צובר אנרגיה פוטנציאלית ואנרגיה זו אינה צריכה להיספג במערכת האבטחה, דבר שמוריד את מקדם הנפילה ואת סך האנרגיה הנספגת במערכת. בנוסף, עקב תנועת המאבטח מתבצעת יותר עבודת חיכוך בחלקי המערכת השונים. לכל הפחות ניתן להגיד שכל מטר שמתרומם המאבטח באוויר, כאילו נפל המטפס מטר אחד פחות.
גם החלקת החבל דרך אביזר החיכוך תורמת להקטנת חומרת הנפילה. בזמן החלקת החבל באביזר החיכוך מתבצעת עבודה באביזר החיכוך (כמו גם בחלקי המערכת האחרים), בהערכה גסה, אם נניח שמחליק כחצי מטר דרך אביזר החיכוך, וכוח הבלימה הוא כ150 קג' כוח, הרי שהחלקה כזו שוות ערך להקטנת אורך הנפילה בכ1 מטר.
חיכוך
חיכוך בטבעות ממיר חלק של האנרגיה לחום. מתבצעת עבודה אשר יש לקחת בחשבון בחישובי האנרגיה. החיכוך בטבעת העליונה משפיע במיוחד על הכוחות מאחר והוא "מפריד" בין החבל הקשור למטפס ובין החבל ההולך לאמצעי החיכוך. קל להבין זאת אם נדמיין טבעת בעלת חיכוך אינסופי, שהחבל אינו זורם בה כלל. במקרה כזה, יימתח רק החבל מצד אחד של הטבעת, זה שמופעל עליו הכוח - זה שעליו תלוי המוביל. הכוח הפועל על המטפס שנפל יגדל, והכוח הפועל על המאבטח יקטן (במידה גדולה יותר מאשר הגדלת הכוח על המטפס).
ניתן לחשב מחדש את הכוחות לקבלת הערכה טובה יותר (וגם זו רק הערכה).
החישובים בעבודה זו מבוססים על עבודתו של Stephen W. Attaway שכתב לזכרם של שלושה חברים אשר נהרגו בנפילה של 259 מטר ב23 ביוני 1996 (סיפור המקרה הופיע במגזין Climbing).
קריאה נוספת
קישורים חיצוניים
תרמו לדף זה: מיכה יניב, דורון נצר, ארנון נצר ואחרים...