הבדלים בין גרסאות בדף "איך עובדים אמצעי חיכוך?"

מתוך Climbing_Encyclopedia
קפיצה אל: ניווט, חיפוש
(←‏קישורים חיצוניים)
 
(104 גרסאות ביניים של 3 משתמשים אינן מוצגות)
שורה 1: שורה 1:
−
=מאמר בעבודה!=
+
'''העיקרון הבסיסי על פיו פועל רובם המכריע של [[אמצעי חיכוך|אמצעי החיכוך]]''' מודגם יפה על ידי [[חבלים|חבל]] המלופף על תוף. הרעיון של אמצעי החיכוך הוא לגרום לחבל להפעיל כוח בניצב לאביזר, וכך ליצור כוח [[חיכוך]]. ככל שהחיכוך גדול יותר, כך נדרש [[אבטחה|המאבטח]] להפעיל פחות כוח בהחזקת החבל מאחורי אמצעי החיכוך, ויותר כוח מועבר ל[[עגינות|עגינה]]. הדרך לעשות זאת היא ליצור "שבירה" (למעשה - ליפוף) של החבל סביב משהו: תוף, [[טבעות|טבעת]], עמוד, אמצעי חיכוך.
−
אופן הפעולה של רובם המכריע של אמצעי החיכוך מודגם יפה על ידי חבל המלופף על תוף. הרעיון של אמצעי החיכוך הוא לגרום לחבל להפעיל כוח בניצב לאביזר, וכך ליצור כוח חיכוך. ככל שהחיכוך גדול יותר, כך נדרש להפעיל פחות כוח בהחזקת החבל. הדרך לעשות זאת היא ליצור "שבירה" של החבל סביב משהו: תוף, טבעת, עמוד, אמצעי חיכוך.
 
  
−
כדי להבין זאת נסתכל על [[חיכוך|כוח החיכוך]] על אלמנט אורך חבל על תוף:
+
המאמר באנגלית: [[?How do friction devices work]]
  
 +
אותו עיקרון פועל גם לאורכו של חבל המתחכך בסלע.
 +
==תזכורת בענייני חיכוך, וחישוב פשוט==
 +
תזכורת קצרה: כוח החיכוך ניתן על ידי: <math>F_f=\mu F_N</math>. כאשר: <math>\mu</math> נקרא מקדם החיכוך והוא תכונה של שני החומרים של הגופים הבאים במגע, ו <math>F_N</math>, הכוח הנורמלי, הוא הכוח הניצב למישור המגע בין שני הגופים.
  
−
(תזכורת קצרה: כוח החיכוך ניתן על ידי: <math>F_f=\mu F_N</math>. כאשר: <math>\mu</math> נקרא מקדם החיכוך והוא תכונה של שני החמרים של הגופים הבאים במגע, ו <math>F_N</math>, הכוח הנורמלי, הוא הכוח הניצב למישור המגע בין שני הגופים).
+
כדי להבין את המשך המאמר אין צורך להתעמק בפיתוח המתמטי-פיזיקלי. המאותגרים מתמטית מוזמנים לקחת את הנוסחה הסופית, ולדלג על החישובים, ישר לדוגמאות.
 +
[[תמונה: capstan3.jpg|left|200px]]
  
−
בתוף מקוטר מסויים ומעלה, אין השפעה לאורך החבל המתחכך בתוף (ולכן אין השפעה לקוטר התוף), אלא לזוית שעובר החבל סביב התוף.
+
נסתכל על [[חיכוך|כוח החיכוך]] על אלמנט אורך חבל על תוף:
  
−
אם נסמן את הזוית ב  <math>\alpha</math>, ואת העומס על החבל ב <math>T_2</math>, נקבל כי הכוח בו צריך למשוך את החבל בצד השני של התוף math>T_1</math> הוא:
+
כשאלמנט אורך (קטע קצר) של חבל עובר על חלק של תוף עגול, ניתן לחשב בקלות את החיכוך על ידי הנוסחה הרגילה. נניח שהקטע שנוגע בחבל הוא כלכך קצר, שהוא בקירוב ישר. הציור מתאר את הכוחות הפועלים עליו:
  
−
<math>T_2=T_1\times e^ \alpha</math>
+
הכוח הנורמאלי <math>F_N</math> הוא פעמיים הרכיב של המתיחות <math>T</math> בכיוון מרכז התוף. רכיב זה מסומן <math>T_y</math>, והוא שווה ל:
 +
 
 +
<math>T_y=\mu T\sin\frac{\alpha}{2}</math>
 +
 
 +
ולכן כוח החיכוך הוא:
 +
 
 +
<math>F_f=\mu F_N=2 \mu T_y\,\!</math>
 +
 
 +
או, בהצבה של <math>F_N</math>:
 +
 
 +
<math>F_f=2\mu T \sin\frac{\alpha}{2}</math>
 +
[[תמונה: capstan1.jpg|left|150px]]
 +
כוח החיכוך מתנגד להחלקה של החבל על התוף, ולמעשה המתיחויות בשני צידי התוף אינה זהה. התמונה הבאה היא יותר אמיתית:
 +
 
 +
המתיחות בחבל הקרוב למשקולת, הוא המשקל, לכן: <math>T_2=w</math>.
 +
 
 +
המתיחות אחרי התוף קטנה יותר, ומסומנת כאן <math>T_1</math>.
 +
 
 +
כוח החיכוך, <math>F_f</math>, תלוי בכוח הנורמאלי, <math>F_N</math>, שאותו כבר מצאנו.
 +
 
 +
==חישוב קצת יותר מסובך==
 +
[[תמונה: capstan2.jpg|left|270px]]
 +
כשקטע ארוך יותר של חבל עובר על התוף, המתיחות משתנה עם כל אלמנט חבל. שינוי המתיחות <math>dT</math>, מתרחש עם כל שינוי של <math>d\alpha</math> בזווית. נסמן את הכוח הנורמלי שמפעיל אלמנט חבל זה ב-<math>dN</math>. כוח החיכוך הוא הסכום של שינוי המתיחויות (למעשה - אינטגרל) על כל אלמנטי האורך של החבל המתחככים בתוף.
 +
 
 +
במצב שיווי משקל, סכום הכוחות מתאפס, בפרט גם סכום הכוחות בכיוון <math>x</math>:
 +
 
 +
<math>\Sigma F_x=0\,\!</math>
 +
 
 +
<math>T\cos\frac{d\theta}{2}+\mu(dN)-(T+dT)\cos\frac{d\theta}{2}=0</math>
 +
 
 +
מכיוון ש <math>d\theta</math> הוא קטן מאד, והקוסינוס שלו הוא אחד, הביטוי מצטמצם ל:
 +
 
 +
<math>\mu(dN)=dT\,\!</math>
 +
 
 +
בדומה, הכוחות בכיוון y, מתאפסים ומן האילוץ <math>\Sigma F_y=0\,\!</math>, מקבלים:
 +
 
 +
<math>dN-(T+dT)\sin\frac{d\theta}{2}-T\sin\frac{d\theta}{2}=0</math>
 +
 
 +
<math>dN=2T\sin\frac{d\theta}{2}+dT\sin\frac{d\theta}{2}=0</math>
 +
 
 +
מכיוון שסינוס של ביטוי קטן מאד שווה לביטוי עצמו:
 +
 
 +
<math>dN=2T\frac{d\theta}{2}+\frac{dT d\theta}{2}=0</math>
 +
 
 +
ניתן להזניח מכפלה של שני ביטויים קטנים מאד והביטוי מצטמצם ל:
 +
 
 +
<math>dN=Td\theta\,\!</math>
 +
 
 +
אם נציב את <math>dN</math>, נוכל לקבל ביטוי שאינו תלוי בכוחות הנורמאליים והוא משוואה דיפרנציאלית המבטאת את <math>T</math>:
 +
 
 +
<math>\frac{dT}{T}=\mu d\theta\,\!</math>
 +
 
 +
כדי לקבל את ההפרש במתיחות בין הצדדים, יש לסכום (לאנטגרל) על זווית המגע הכללית בין החבל לבין התוף:
 +
 
 +
<math>\int_{T_1}^{T_2}\frac{dT}{T} = \int_0^\alpha \mu d\theta</math>
 +
 
 +
וvאינטגרציה נותנת:
 +
 
 +
<math>\ln\frac{T_1}{T_2} = \mu\alpha</math>
 +
 
 +
הכוח בו צריך למשוך את החבל בצד השני של התוף <math>T_1</math> הוא:
 +
 
 +
<math>T_1=T_2e^{\mu\alpha}\,\!</math>
  
 
וכוח החיכוך הוא ההפרש בין המתיחויות בחבל בשני צידי התוף:
 
וכוח החיכוך הוא ההפרש בין המתיחויות בחבל בשני צידי התוף:
  
−
<math>T_2=T_1\times e^ \alpha</math>
+
<math>F_f=T_2(1-e^{\mu\alpha})\,\!</math>
 +
 
 +
למעשה, בתוף מקוטר מסויים ומעלה, אין השפעה לאורך החבל המתחכך בתוף (ולכן גם אין השפעה לקוטר התוף), אלא רק לזוית שעובר החבל סביב התוף.
 +
 
 +
==סיכום ביניים==
 +
[[תמונה: capstan4.jpg|left|200px]]
 +
קיבלנו כי החיכוך של חבל על תוף עגול מושפע משלושה גורמים:
 +
* המתיחות בחבל.
 +
* מקדם החיכוך.
 +
* זווית המגע של החבל והתוף (כמו שמסומן <math>\alpha</math> באיור).
 +
 
 +
החיכוך תלוי באופן ישר במתיחות, ועולה אקספוננציאלית עם זווית המגע ועם מקדם החיכוך. אם נניח כי מקדם החיכוך קבוע, למשל של חבל ניילון עם סגסוגת אלומיניום טיפוסית המשמשת לציוד טיפוס (למשל A7075), נוכל להשוות בין אמצעי חיכוך שונים.
 +
 
 +
חשוב לזכור שמקדם החיכוך תלוי במידה רבה במצב החבל ובתכונותיו. עבור חבל חדש, ועוד יותר מכך, חבל רטוב או מבוצבץ, מקדם החיכוך יהיה נמוך. לחבל בלוי ו"צמרי", יהיה מקדם חיכוך גבוה.
 +
 
 +
הערה לעניין זווית המגע או חלק הסיבוב שעובר החבל סביב התוף. למעשה, זה נכון בתוף מקוטר מסויים ומעלה, אבל זה קירוב טוב לחבלים לא "קשים" החל מתוף שקוטרו דומה לקוטר החבל (כלומר: שמינית, טבעות, [[סולם]] ואמצעי חיכוך אחרים).
 +
 
 +
המצב שונה מעט באמצעי חיכוך כמו [[ATC]], [[רברסו]] ואחרים, בהם החבל עובר ביציאה, במצב נעילה, סביב "מוט" שקוטרו קטן יותר (אנחנו אומרים - השבירה חדה יותר). במקרה כזה החישוב יהיה שונה. החבל יוצר מעין צורת  "ח". יש קטע קצר של חבל שנלחץ אל אמצעי החיכוך, ושני קטעים בצדדים, שכמעט ולא נוגעים. אם מניחים שהחבל קשיח למדי, מופעל במצב שיווי משקל כוח נורמאלי כמעט כפול מן המתיחות בחבל, והחיכוך גדול מאד.
 +
 
 +
עניין אחרון, הזווית <math>\alpha</math> במשוואה, היא ביחידות של רדיאנים. אם רוצים להציב ערכים ולקבל תוצאה מספרית, אלו היחידות בהן צריך להשתמש.
 +
 
 +
נזכיר כי רדיאן אחד הוא הזווית בה אורך הקשת שווה לרדיוס. מכיוון שהיחס בין הרדיוס להיקף הוא <math>2\pi</math>, הרי שזווית המגע על פני סיבוב שלם, 360°, היא  <math>2\pi</math> רדיאנים, או 6.28 רדיאנים, בערך. רדיאן אחד שווה בערך ל-57.29°.
 +
 
 +
==דוגמאות==
 +
הערכים המספריים, והיחסים בין המתיחויות לפני ואחרי אמצעי החיכוך חושבו עם מקדם חיכוך של <math> \mu = 0.25</math>.
 +
 
 +
===דוגמה 0: טבעת עליונה===
 +
[[תמונה: friction in binner.jpg|שמאל|ממוזער|160px|חבל עובר על טבעת]]
 +
זה המקרה הכי בסיסי: חבל שעובר בטבעת עם חבל עגול בקירוב. זהו המצב ב[[טופ-רופ]], במשיכת חבל ב[[גולש אחרון]] ובנפילת [[הובלה]]. הפרש הזויות במעבר של חבל על טבעת הוא 180°. בחישוב מתקבל היחס בין המתיחויות בשני צידי החבל על פי
 +
<math>\frac{T_1}{T_2}=e^{\mu \pi}=e^{0.25*3.14}\approx 1.48</math>
 +
כלומר - הבדל של כ-50%.
 +
 
 +
===דוגמה 1: מוט עגול, צינור או [[טיובה]]===
 +
[[תמונה: friction in tube.jpg|left|320px]]
 +
התמונה מסבירה את עצמה הכי טוב, כנראה. ניתן לראות את הזווית גדלה, ואיתה החיכוך. כל ליפוף נוסף של החבל על הצינור של הטיובה מוסיף 360° או <math>2\pi</math> רדיאנים.
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
===דוגמה 2: [[סולם]]===
 +
[[תמונה: friction in rack.jpg|left|420px]]
 +
בסולם יש שתי אפשרויות עיקריות להגדיל את החיכוך.
 +
 
 +
האפשרות הראשונה, על ידי הוספת שלבים לסולם. בצורה זו גדלה זווית המגע הכללית במידה קבועה עם כל תוספת של מוט לסולם.
 +
 
 +
האפשרות השניה מגדילה את הזווית על ידי קירובם של השלבים זה לזה. ציפוף של השלבים מכריח את החבל להתלפף יותר סביב המוטות וזוית המגע גדלה.
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
===דוגמה 3: [[שמינית]]===
 +
[[תמונה: Eight_friction.jpg|left|350px]]
 +
אם בוחנים את מעבר החבל בשמינית מגלים שבמצב בו יש מינימום חיכוך, שבו "קל" לתת חבל, יש זווית מגע של 540° (180°+180°+180°), או <math>3\pi</math> רדיאנים.
 +
 
 +
במצב "נעול", כלומר עם חיכוך מקסימאלי, במקום 180°, ביציאה מהשמינית, יש 270°, ובסך הכל 630° או <math>3.5\pi</math> רדיאנים.
 +
 
 +
בשמינית, אם כן, בין המצבים של מינימום ומקסימום חיכוך על פי משוואת התוף, יש הבדל של 16.66% בלבד. ידוע כי בשמינית קשה לקחת ולתת חבל במהירות גם במצב של חיכוך מינימאלי. מאידך, ההבדל הקטן יחסית ביו שני המצבים הופל את השמינית אמצעי טוב לגלישה: גם במצב "פתוח" אין זרימה מאד מהירה של חבל, וקל לווסת את כמות החיכוך ביניהם.
 +
 
 +
המעבר בין שני המצבים הוא כמעט רציף.
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
===דוגמה 4: [[שטיכט]]===
 +
[[תמונה:friction in sticht.jpg|left|350x]]
 +
למרבית אמצעי החיכוך שמבוססים על מבנה של שטיכט יש איזור "שבירה" של החבל בו ה"מוט" עליו עובר החבל במצב נעילה הוא דק בהרבה מקוטר החבל.
 +
 
 +
אם בוחנים את מעבר החבל באמצעי חיכוך כזה, מגלים שבמצב בו יש מינימום חיכוך, יש זווית מגע של 180° בלבד, רק על הטבעת, או זווית של <math>\frac{\pi}{2}</math> רדיאנים. באמצעי חיכוך כאלה קל מאד לקחת ולתת חבל במצב "פתוח", הרבה יותר משמינית.
 +
 
 +
בתמונה מוצגים שני אמצעי חיכוך מקבוצה זו: שטיכט ו[[טיובר]].
 +
 
 +
במצב של "נעילה", החישוב שלנו, כאמור, אינו מהווה קירוב טוב ויש השפעה חזקה לרדיוס העקמומיות של שפת אמצעי החיכוך, ושל ה[[נוטביליטי]] של החבל.
 +
 
 +
 
 +
 
 +
 
 +
 
 +
===דוגמה 5: אמצעים ננעלים אוטומטית===
 +
הכוונה היא ל[[אמצעי חיכוך ננעלים אוטומטית לחבל יחיד|אמצעי חיכוך מורכבים, לחבל יחיד]] כמו [[גריגרי]], [[סטופ]], [[ID]] (אבל גם פשוטים כמו [[טוקאן]], [[רברסו]], [[גלובוס]] ו[[גיגי]] במצב אוטולוק). במצב פתוח, באמצעים אלה, החלקת החבל היא איטית וניתן להעריך את החיכוך על פי העקרונות שהוסברו למעלה, כלומר, לפי זווית המגע של החבל עם התוף. נסו להשוות בין גיגי לגריגרי, במצב פתוח, בתור תרגיל.
 +
 
 +
במצב נעילה, לעומת זאת, המצב שונה. כאן התיאוריה קורסת לחלוטין. באמצעים אלה הנעילה מתבצעת על ידי הגדלה משמעותית של כוח החיכוך בקטע חבל אחד, על ידי לחיצה או צביטה חזקה של החבל. לכן, במצב נעילה אין משמעות לזווית המגע, אלא להמרה של החיכוך בזרימת החבל ללחיצה בניצב לכיוון ההחלקה. אבל זה נושא למאמר אחר...
 +
 
 +
===דוגמה 6: חיכוך בנפילת הובלה===
 +
[[תמונה: friction_lead_fall.jpg|שמאל|ממוזער|180px|הזויות בטבעות של הראנרים בהובלה]]
 +
החיכוך הנוצר ממעבר החבל בטבעות בזמן [[נפילה]] ב[[הובלה]] גורם לכך שעל קטעי חבל שונים יש מתיחות שונה. ניתן להעריך את ההפרש בין הכוח שמרגיש המטפס ([[כוח בלימה|כוח הבלימה]]) לבין הכוח שמרגיש המאבטח. הפרש זה יהיה כוח החיכוך המתפתח בכל הטבעות של כל ה[[ראנרים]] יחד. את הכוח הזה ניתן לחשב על ידי חיבור הזויות של החבל בכל העגינות והצבת הזווית הכללית בנוסחה.
 +
 
 +
מכאן ברור שאם הזוית בעגינה מסויימת חדה, לא רק שלמוביל יהיה [[דראג]] (חיכוך על הסלע ובטבעות), אלא גם שבמקרה של נפילה, זוית חדה בעצם "מפרידה" בין שני קטעי חבל. מקבלים שבמקום [[מקדם הנפילה|מקדם נפילה]] שרגילים לקחת כהערכה לכוח הבלימה, במקרה כזה יש ו[[מקדם נפילה אפקטיבי|מקדם הנפילה האפקטיבי]] שהוא גדול יותר מזה התיאורטי.
 +
 
 +
==קישורים חיצוניים==
 +
*[http://www.wiki.imga.org.il/Papers/att_frict.pdf  המאמר העיקרי עליו מתבסס מאמר זה]
 +
*[http://www.wiki.imga.org.il/Papers/mechanics.pdf עוד מאמר אחד, גם על חיכוך בסוגי סלעים שונים]
 +
*ב[http://www.xmission.com/~tmoyer/testing/Simulation_of_Climbing_and_Rescue_Belays.pdf מאמר הזה] יש ניתוח של כוחות באמצעי חיכוך, בכל מיני מצבים: טיפוס, גלישה, חילוץ.
 +
 
 +
----
 +
תרמו לדף זה: [[משתמש: מיכה יניב|מיכה יניב]] ואחרים...
 +
 
 +
[[קטגוריה: טיפוס הרים]][[קטגוריה: טיפוס]][[קטגוריה: טיפוס סלע]][[קטגוריה: הגדרות]][[קטגוריה: אמצעי חיכוך]][[קטגוריה: טיפוס ספורטיבי]][[קטגוריה: ציוד טיפוס הרים]][[קטגוריה: ציוד טיפוס]][[קטגוריה: ציוד טיפוס סלע]][[קטגוריה: ציוד טיפוס ספורטיבי]][[קטגוריה: הכה את המומחה]][[קטגוריה: מאמרים מתורגמים ומקוריים]]

גרסה אחרונה מ־07:49, 25 ביולי 2020

העיקרון הבסיסי על פיו פועל רובם המכריע של אמצעי החיכוך מודגם יפה על ידי חבל המלופף על תוף. הרעיון של אמצעי החיכוך הוא לגרום לחבל להפעיל כוח בניצב לאביזר, וכך ליצור כוח חיכוך. ככל שהחיכוך גדול יותר, כך נדרש המאבטח להפעיל פחות כוח בהחזקת החבל מאחורי אמצעי החיכוך, ויותר כוח מועבר לעגינה. הדרך לעשות זאת היא ליצור "שבירה" (למעשה - ליפוף) של החבל סביב משהו: תוף, טבעת, עמוד, אמצעי חיכוך.

המאמר באנגלית: ?How do friction devices work

אותו עיקרון פועל גם לאורכו של חבל המתחכך בסלע.

תזכורת בענייני חיכוך, וחישוב פשוט

תזכורת קצרה: כוח החיכוך ניתן על ידי: עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): F_f=\mu F_N . כאשר: עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \mu נקרא מקדם החיכוך והוא תכונה של שני החומרים של הגופים הבאים במגע, ו עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): F_N , הכוח הנורמלי, הוא הכוח הניצב למישור המגע בין שני הגופים.

כדי להבין את המשך המאמר אין צורך להתעמק בפיתוח המתמטי-פיזיקלי. המאותגרים מתמטית מוזמנים לקחת את הנוסחה הסופית, ולדלג על החישובים, ישר לדוגמאות.

Capstan3.jpg

נסתכל על כוח החיכוך על אלמנט אורך חבל על תוף:

כשאלמנט אורך (קטע קצר) של חבל עובר על חלק של תוף עגול, ניתן לחשב בקלות את החיכוך על ידי הנוסחה הרגילה. נניח שהקטע שנוגע בחבל הוא כלכך קצר, שהוא בקירוב ישר. הציור מתאר את הכוחות הפועלים עליו:

הכוח הנורמאלי עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): F_N הוא פעמיים הרכיב של המתיחות עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): T בכיוון מרכז התוף. רכיב זה מסומן עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): T_y , והוא שווה ל:

עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): T_y=\mu T\sin\frac{\alpha}{2}

ולכן כוח החיכוך הוא:

עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): F_f=\mu F_N=2 \mu T_y\,\!

או, בהצבה של עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): F_N :

עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): F_f=2\mu T \sin\frac{\alpha}{2}

Capstan1.jpg

כוח החיכוך מתנגד להחלקה של החבל על התוף, ולמעשה המתיחויות בשני צידי התוף אינה זהה. התמונה הבאה היא יותר אמיתית:

המתיחות בחבל הקרוב למשקולת, הוא המשקל, לכן: עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): T_2=w .

המתיחות אחרי התוף קטנה יותר, ומסומנת כאן עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): T_1 .

כוח החיכוך, עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): F_f , תלוי בכוח הנורמאלי, עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): F_N , שאותו כבר מצאנו.

חישוב קצת יותר מסובך

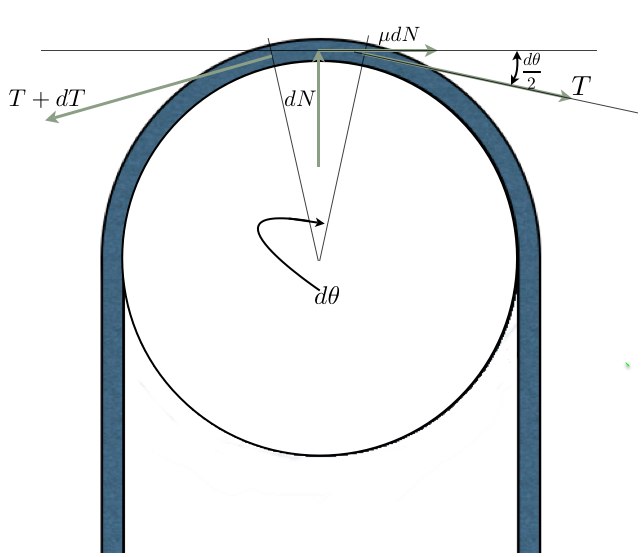
Capstan2.jpg

כשקטע ארוך יותר של חבל עובר על התוף, המתיחות משתנה עם כל אלמנט חבל. שינוי המתיחות עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): dT , מתרחש עם כל שינוי של עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): d\alpha בזווית. נסמן את הכוח הנורמלי שמפעיל אלמנט חבל זה ב-עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): dN . כוח החיכוך הוא הסכום של שינוי המתיחויות (למעשה - אינטגרל) על כל אלמנטי האורך של החבל המתחככים בתוף.

במצב שיווי משקל, סכום הכוחות מתאפס, בפרט גם סכום הכוחות בכיוון עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): x :

עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \Sigma F_x=0\,\!

עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): T\cos\frac{d\theta}{2}+\mu(dN)-(T+dT)\cos\frac{d\theta}{2}=0

מכיוון ש עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): d\theta הוא קטן מאד, והקוסינוס שלו הוא אחד, הביטוי מצטמצם ל:

עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \mu(dN)=dT\,\!

בדומה, הכוחות בכיוון y, מתאפסים ומן האילוץ עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \Sigma F_y=0\,\! , מקבלים:

עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): dN-(T+dT)\sin\frac{d\theta}{2}-T\sin\frac{d\theta}{2}=0

עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): dN=2T\sin\frac{d\theta}{2}+dT\sin\frac{d\theta}{2}=0

מכיוון שסינוס של ביטוי קטן מאד שווה לביטוי עצמו:

עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): dN=2T\frac{d\theta}{2}+\frac{dT d\theta}{2}=0

ניתן להזניח מכפלה של שני ביטויים קטנים מאד והביטוי מצטמצם ל:

עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): dN=Td\theta\,\!

אם נציב את עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): dN , נוכל לקבל ביטוי שאינו תלוי בכוחות הנורמאליים והוא משוואה דיפרנציאלית המבטאת את עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): T :

עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \frac{dT}{T}=\mu d\theta\,\!

כדי לקבל את ההפרש במתיחות בין הצדדים, יש לסכום (לאנטגרל) על זווית המגע הכללית בין החבל לבין התוף:

עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \int_{T_1}^{T_2}\frac{dT}{T} = \int_0^\alpha \mu d\theta

וvאינטגרציה נותנת:

עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \ln\frac{T_1}{T_2} = \mu\alpha

הכוח בו צריך למשוך את החבל בצד השני של התוף עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): T_1 הוא:

עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): T_1=T_2e^{\mu\alpha}\,\!

וכוח החיכוך הוא ההפרש בין המתיחויות בחבל בשני צידי התוף:

עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): F_f=T_2(1-e^{\mu\alpha})\,\!

למעשה, בתוף מקוטר מסויים ומעלה, אין השפעה לאורך החבל המתחכך בתוף (ולכן גם אין השפעה לקוטר התוף), אלא רק לזוית שעובר החבל סביב התוף.

סיכום ביניים

Capstan4.jpg

קיבלנו כי החיכוך של חבל על תוף עגול מושפע משלושה גורמים:

  • המתיחות בחבל.
  • מקדם החיכוך.
  • זווית המגע של החבל והתוף (כמו שמסומן עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \alpha באיור).

החיכוך תלוי באופן ישר במתיחות, ועולה אקספוננציאלית עם זווית המגע ועם מקדם החיכוך. אם נניח כי מקדם החיכוך קבוע, למשל של חבל ניילון עם סגסוגת אלומיניום טיפוסית המשמשת לציוד טיפוס (למשל A7075), נוכל להשוות בין אמצעי חיכוך שונים.

חשוב לזכור שמקדם החיכוך תלוי במידה רבה במצב החבל ובתכונותיו. עבור חבל חדש, ועוד יותר מכך, חבל רטוב או מבוצבץ, מקדם החיכוך יהיה נמוך. לחבל בלוי ו"צמרי", יהיה מקדם חיכוך גבוה.

הערה לעניין זווית המגע או חלק הסיבוב שעובר החבל סביב התוף. למעשה, זה נכון בתוף מקוטר מסויים ומעלה, אבל זה קירוב טוב לחבלים לא "קשים" החל מתוף שקוטרו דומה לקוטר החבל (כלומר: שמינית, טבעות, סולם ואמצעי חיכוך אחרים).

המצב שונה מעט באמצעי חיכוך כמו ATC, רברסו ואחרים, בהם החבל עובר ביציאה, במצב נעילה, סביב "מוט" שקוטרו קטן יותר (אנחנו אומרים - השבירה חדה יותר). במקרה כזה החישוב יהיה שונה. החבל יוצר מעין צורת "ח". יש קטע קצר של חבל שנלחץ אל אמצעי החיכוך, ושני קטעים בצדדים, שכמעט ולא נוגעים. אם מניחים שהחבל קשיח למדי, מופעל במצב שיווי משקל כוח נורמאלי כמעט כפול מן המתיחות בחבל, והחיכוך גדול מאד.

עניין אחרון, הזווית עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \alpha במשוואה, היא ביחידות של רדיאנים. אם רוצים להציב ערכים ולקבל תוצאה מספרית, אלו היחידות בהן צריך להשתמש.

נזכיר כי רדיאן אחד הוא הזווית בה אורך הקשת שווה לרדיוס. מכיוון שהיחס בין הרדיוס להיקף הוא עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): 2\pi , הרי שזווית המגע על פני סיבוב שלם, 360°, היא עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): 2\pi רדיאנים, או 6.28 רדיאנים, בערך. רדיאן אחד שווה בערך ל-57.29°.

דוגמאות

הערכים המספריים, והיחסים בין המתיחויות לפני ואחרי אמצעי החיכוך חושבו עם מקדם חיכוך של עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \mu = 0.25 .

דוגמה 0: טבעת עליונה

חבל עובר על טבעת

זה המקרה הכי בסיסי: חבל שעובר בטבעת עם חבל עגול בקירוב. זהו המצב בטופ-רופ, במשיכת חבל בגולש אחרון ובנפילת הובלה. הפרש הזויות במעבר של חבל על טבעת הוא 180°. בחישוב מתקבל היחס בין המתיחויות בשני צידי החבל על פי עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \frac{T_1}{T_2}=e^{\mu \pi}=e^{0.25*3.14}\approx 1.48 כלומר - הבדל של כ-50%.

דוגמה 1: מוט עגול, צינור או טיובה

Friction in tube.jpg

התמונה מסבירה את עצמה הכי טוב, כנראה. ניתן לראות את הזווית גדלה, ואיתה החיכוך. כל ליפוף נוסף של החבל על הצינור של הטיובה מוסיף 360° או עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): 2\pi רדיאנים.






דוגמה 2: סולם

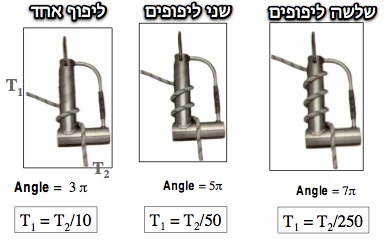
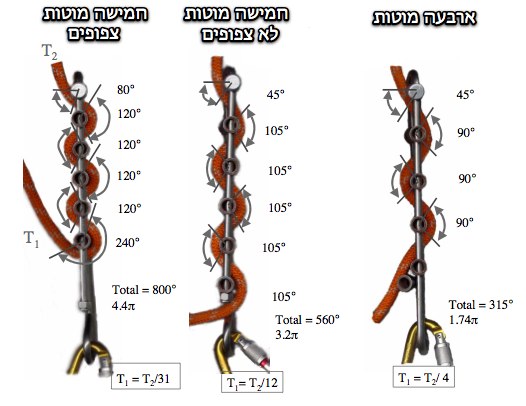
Friction in rack.jpg

בסולם יש שתי אפשרויות עיקריות להגדיל את החיכוך.

האפשרות הראשונה, על ידי הוספת שלבים לסולם. בצורה זו גדלה זווית המגע הכללית במידה קבועה עם כל תוספת של מוט לסולם.

האפשרות השניה מגדילה את הזווית על ידי קירובם של השלבים זה לזה. ציפוף של השלבים מכריח את החבל להתלפף יותר סביב המוטות וזוית המגע גדלה.








דוגמה 3: שמינית

Eight friction.jpg

אם בוחנים את מעבר החבל בשמינית מגלים שבמצב בו יש מינימום חיכוך, שבו "קל" לתת חבל, יש זווית מגע של 540° (180°+180°+180°), או עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): 3\pi רדיאנים.

במצב "נעול", כלומר עם חיכוך מקסימאלי, במקום 180°, ביציאה מהשמינית, יש 270°, ובסך הכל 630° או עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): 3.5\pi רדיאנים.

בשמינית, אם כן, בין המצבים של מינימום ומקסימום חיכוך על פי משוואת התוף, יש הבדל של 16.66% בלבד. ידוע כי בשמינית קשה לקחת ולתת חבל במהירות גם במצב של חיכוך מינימאלי. מאידך, ההבדל הקטן יחסית ביו שני המצבים הופל את השמינית אמצעי טוב לגלישה: גם במצב "פתוח" אין זרימה מאד מהירה של חבל, וקל לווסת את כמות החיכוך ביניהם.

המעבר בין שני המצבים הוא כמעט רציף.






דוגמה 4: שטיכט

350x

למרבית אמצעי החיכוך שמבוססים על מבנה של שטיכט יש איזור "שבירה" של החבל בו ה"מוט" עליו עובר החבל במצב נעילה הוא דק בהרבה מקוטר החבל.

אם בוחנים את מעבר החבל באמצעי חיכוך כזה, מגלים שבמצב בו יש מינימום חיכוך, יש זווית מגע של 180° בלבד, רק על הטבעת, או זווית של עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \frac{\pi}{2} רדיאנים. באמצעי חיכוך כאלה קל מאד לקחת ולתת חבל במצב "פתוח", הרבה יותר משמינית.

בתמונה מוצגים שני אמצעי חיכוך מקבוצה זו: שטיכט וטיובר.

במצב של "נעילה", החישוב שלנו, כאמור, אינו מהווה קירוב טוב ויש השפעה חזקה לרדיוס העקמומיות של שפת אמצעי החיכוך, ושל הנוטביליטי של החבל.



דוגמה 5: אמצעים ננעלים אוטומטית

הכוונה היא לאמצעי חיכוך מורכבים, לחבל יחיד כמו גריגרי, סטופ, ID (אבל גם פשוטים כמו טוקאן, רברסו, גלובוס וגיגי במצב אוטולוק). במצב פתוח, באמצעים אלה, החלקת החבל היא איטית וניתן להעריך את החיכוך על פי העקרונות שהוסברו למעלה, כלומר, לפי זווית המגע של החבל עם התוף. נסו להשוות בין גיגי לגריגרי, במצב פתוח, בתור תרגיל.

במצב נעילה, לעומת זאת, המצב שונה. כאן התיאוריה קורסת לחלוטין. באמצעים אלה הנעילה מתבצעת על ידי הגדלה משמעותית של כוח החיכוך בקטע חבל אחד, על ידי לחיצה או צביטה חזקה של החבל. לכן, במצב נעילה אין משמעות לזווית המגע, אלא להמרה של החיכוך בזרימת החבל ללחיצה בניצב לכיוון ההחלקה. אבל זה נושא למאמר אחר...

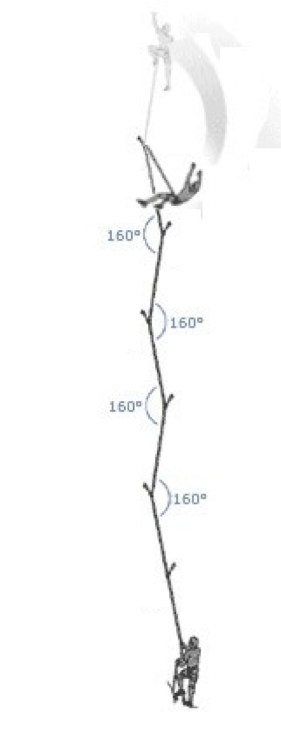
דוגמה 6: חיכוך בנפילת הובלה

הזויות בטבעות של הראנרים בהובלה

החיכוך הנוצר ממעבר החבל בטבעות בזמן נפילה בהובלה גורם לכך שעל קטעי חבל שונים יש מתיחות שונה. ניתן להעריך את ההפרש בין הכוח שמרגיש המטפס (כוח הבלימה) לבין הכוח שמרגיש המאבטח. הפרש זה יהיה כוח החיכוך המתפתח בכל הטבעות של כל הראנרים יחד. את הכוח הזה ניתן לחשב על ידי חיבור הזויות של החבל בכל העגינות והצבת הזווית הכללית בנוסחה.

מכאן ברור שאם הזוית בעגינה מסויימת חדה, לא רק שלמוביל יהיה דראג (חיכוך על הסלע ובטבעות), אלא גם שבמקרה של נפילה, זוית חדה בעצם "מפרידה" בין שני קטעי חבל. מקבלים שבמקום מקדם נפילה שרגילים לקחת כהערכה לכוח הבלימה, במקרה כזה יש ומקדם הנפילה האפקטיבי שהוא גדול יותר מזה התיאורטי.

קישורים חיצוניים

תרמו לדף זה: מיכה יניב ואחרים...

אוחזר מתוך "https://wiki.imga.org.il/index.php?title=איך_עובדים_אמצעי_חיכוך%3F&oldid=15605"