הבדלים בין גרסאות בדף "ריכוז מאמצים"
(←עקומת מאמץ-מעוות) |
מ (החלפת טקסט - קטגוריה:כללי ל־'') |
||
| (27 גרסאות ביניים של 2 משתמשים אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
| − | + | [[תמונה: stressconcentration.jpg|left|300px]] | |
| − | ''' | + | '''ריכוז מאמצים''' (באנגלית: '''[[stress concentration]]''') הוא תופעה המתרחשת כאשר כוח פועל על גוף ששטח החתך שלו משתנה. אם ניקח, לדוגמה, קורה רבועה שיש בה חור, ומופעלים עליה כוחות משיכה. שטח החתך בכל מקום לאורך הקורה הוא קבוע מלבד באיזור החור. החומר "מרגיש" [[מאמצים|מאמץ מתיחה]]. ה[[מאמצים|מאמץ]] מוגדר על ידי כוח ליחידת שטח: |
| − | מאמץ מתיחה | + | מאמץ מתיחה מחושב על ידי <math>\sigma=\frac{F}{A}</math> |
כאשר: <math>\sigma</math> - ערך המאמץ, <math>F</math> - ערך הכוח הפועל, <math>A</math> - שטח חתך הגוף. | כאשר: <math>\sigma</math> - ערך המאמץ, <math>F</math> - ערך הכוח הפועל, <math>A</math> - שטח חתך הגוף. | ||
| − | ניתן לראות שככל שהכוח הפועל על הגוף גדל, גדל גם המאמץ ואילו ככל ששטח החתך גדל, המאמץ קטן | + | ניתן לראות שככל שהכוח הפועל על הגוף גדל, גדל גם המאמץ ואילו ככל ששטח החתך גדל, המאמץ קטן. |
| − | |||
| − | |||
| − | + | נחזור לקורה: באיזור ה"מופרע", זה שיש בו את החור, שטח החתך של הקורה קטן יותר, ולכן המאמץ שם גדול יותר. | |
| − | |||
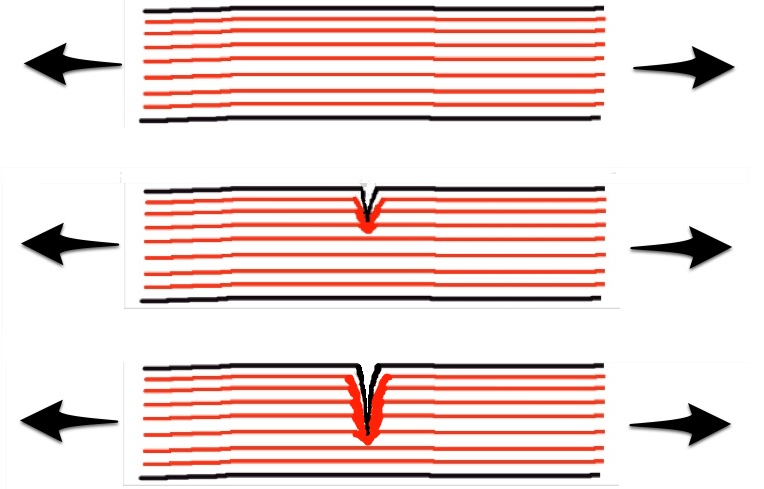
| − | + | אם שטח החתך קבוע (כמו בגליל, או בתיבה) המאמץ נשאר קבוע בכל מקום. בגוף ששטח החתך שלו שונה במקומות שונים (כמו במוט שניסרו או שייפו את היקפו), נוצר ריכוז של המאמצים: הכוח פועל על שטח חתך שגודלו משתנה (קטן) ומתקבל מאמץ גדל. התמונה מראה שלוש דוגמאות של שינוי בשטח החתך והגידול במאמץ כתוצאה מכך. | |
| + | =השפעת ריכוז המאמצים= | ||
| + | [[תמונה: stressconcentration2.jpg|שמאל|ממוזער|300px|דוגמאות שונות לריכוז מאמצים]] | ||
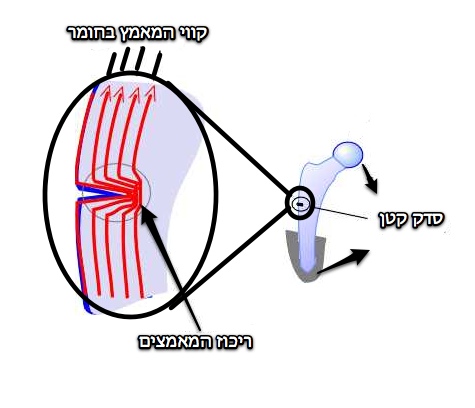
| + | כאשר המאמץ בנקודה מסוימת יעלה על יכולת החומר להתנגד לו, החומר יקרוס וישבר או ייקרע. ריכוז מאמצים נוצר במקרים רבים סביב פגמים בחומר, חורים קטנים או סדקים. ריכוז המאמצים גורם להגדלת הפגמים והסדקים, עד לשבירה של החומר כולו. | ||
| − | + | ניתן לתאר זאת על ידי הדמיה של קווי מעבר הכוח - הקווים לארכם עובר הכוח דרך החומר. במקום בו יש חור, סדק או פגם, שטח החתך קטן יותר. קווי הכוח חייבים להצטופף בשטח קטן יותר ומתקבל יותר כוח ליחידה שטח - מאמץ גדול יותר המתרכז בנקודה מסויימת. אם המאמץ גדול יותר מזה שהחומר יכול לשאת, הוא קורס. | |
| − | + | =ריכוז מאמצים בטיפוס= | |
| − | + | ==ריכוז מאמצים ב[[קשרים]]== | |
| − | ( | + | ==ריכוז מאמצים ב[[אבני עיגון]]== |
| − | == | + | תופעת ריכוז המאמצים באה לידי ביטוי במגע בין אבני עיגון ובין הסלע. העניין חשוב בכל אבן עיגון, אך במיוחד באבני עיגון פאסיביות (רוקים). ההנחיה הכללית היא להשתמש ברוקים כך ששטח המגע בין העגינה לבין הסלע הוא מקסימאלי. הרעיון הוא שככל ששטח המגע גדול, כך המאמץ קטן. אם השטח קטן, נאמר רוק שיושב על ארבעה זיזים קטנים של סלע, כל המאמץ יתרכז בהם והסיכוי שאחד מהם יישבר והעגינה תצא - גדול. זה נכון גם לפרנדים, טריקמים וכל עגינה אחרת. |
| − | [[תמונה: | + | ==קריעת נייר ב[[רצועות]]== |
| − | + | [[תמונה: webbingtear1.jpg|שמאל|ממוזער|300px|התפתחות של קריעת נייר ברצועה]] | |
| + | קריעת נייר ברצועות דומה במקצת לריכוז מאמצים בתוך קשר, אבל היא מקרה קיצוני יותר בגלל המבנה השטוח של הרצועות. המבנה גורם לכך שכל קרע קטן בשפה של רצועה עלול לגדול במהירות ולהפוך לכשל של כל הרצועה. גם כאן, הריכוז של קווי הכוח בקצה הקרע מתבטא בריכוז מאמצי המתיחה בשטח קטן, ואיזור זה נקרע. ככל שהקרע גדל, יותר קוי כוח מתרכזים בקצה הקרע ושוב, הקרע גדל. | ||
| − | + | זה דומה לכשל בגלל ריכוז מאמצים בקורה קשיחה, אבל שוב, קיצוני יותר כי הרצועה אינה קשיחה והחלק הקרוע יכול להיפתח ולהעביר את הכוח לקצה של הקרע יותר בקלות. ברצועות, בניגוד לקורות, יש הבדל במיקום הפגם ופגמים על השפה מחלישים את הרצועה הרבה יותר מחור באמצע הרצועה, למשל. חשוב להזכיר גם שרצועות מתמודדות היטב עם מאמצי מתיחה, והן משנות את צורתן כמעט ללא התנגדות תחת מאמצים אחרים: דחיסה, כפיפה ופיתול. | |
| − | + | עןד תופעה מתרחשת במקרים שבהם הרצועה נמשכת לא לארכה אלא באופן שקצת מעוות אותה. במקרה כזה, רק חלק קטן משטח הרצועה נושא את העומס וכל המאמץ מתרכז שם. זה דומה לקריעה של פלסטר או רצועת פלנלית, רק ששם אנחנו בכוונה מתחילים מן השפה, כדי שיהיה לנו יותר קל לקרוע אותה. | |
| + | [[תמונה: webbingtear2.jpg|שמאל|ממוזער|150px|קשר משקפים ברצועה סביב עמוד]] | ||
| − | + | [[תמונה: webbingtear3.jpg|שמאל|ממוזער|220px|רצועת [[דיינימה]] שנקרעה בקשר משקפים]] | |
| − | |||
| − | + | ב[[קשרים]] ברצועות, במיוחד קשרי חביקה כמו ב[[:קטגוריה: קביעות|קביעה]] הנבנית משתי רצועות שלובות זו בזו, או מרצועה וחבל (girth hitch) או רצועה וכבל. זה דומה גם בקשר הנראה בתמונה של רצועה על מוט, שנקרא [[קשר משקפים]] או לפעמים "קשר סכין", ובו הרצועה עלולה לחתוך את עצמה. | |
| − | + | בקשר כזה, מקבלים את שתי התופעות שתוארו. קודם כל, השפה של הרצועה נשחקת תחת עומס ברצועה האחרת (או בחבל או בכבל). זה גורם להופעה של קרעים קטנים בשפת הרצועה. בהמשך, הקרעים הקטנים גדלים במהירות עד לכשל של הרצועה. בתמונה נראית רצועת [[דיינימה]] שנקרעה בקשר כזה תחת משקל גוף! | |
| − | + | קיימת טענה מקובלת ש[[רצועות#רצועות טובולריות|רצועות טובולריות]] רגישות פחות לקריעת נייר מ[[רצועות#רצועות שטוחות|רצועות שטוחות]]. זה בגלל שלרצועות טובולריות אין ממש שפה. הן שטוחות בכיוון הזה רק מתוך מקריות, ולמעשה אפשר להרחיק כל קרע קטן מן השפה על ידי גלגול הרצועה, כך שלא יהיה על השפה אלא יותר כמו חור באמצע הרצועה. | |
| − | + | ==קישורים חיצוניים== | |
| − | |||
| − | + | ---- | |
| + | תרמו לדף זה: [[משתמש: מיכה יניב|מיכה יניב]], [[משתמש: שחר קדמיאל|שחר קדמיאל]] ואחרים... | ||
| − | + | [[קטגוריה:טכניקות ומיומנויות]][[קטגוריה:ציוד]][[קטגוריה:ציוד טיפוס]][[קטגוריה: טיפוס]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
גרסה אחרונה מ־04:27, 18 באוגוסט 2010
ריכוז מאמצים (באנגלית: stress concentration) הוא תופעה המתרחשת כאשר כוח פועל על גוף ששטח החתך שלו משתנה. אם ניקח, לדוגמה, קורה רבועה שיש בה חור, ומופעלים עליה כוחות משיכה. שטח החתך בכל מקום לאורך הקורה הוא קבוע מלבד באיזור החור. החומר "מרגיש" מאמץ מתיחה. המאמץ מוגדר על ידי כוח ליחידת שטח:
מאמץ מתיחה מחושב על ידי עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \sigma=\frac{F}{A}
כאשר: עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \sigma - ערך המאמץ, עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): F - ערך הכוח הפועל, עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): A - שטח חתך הגוף.
ניתן לראות שככל שהכוח הפועל על הגוף גדל, גדל גם המאמץ ואילו ככל ששטח החתך גדל, המאמץ קטן.
נחזור לקורה: באיזור ה"מופרע", זה שיש בו את החור, שטח החתך של הקורה קטן יותר, ולכן המאמץ שם גדול יותר.
אם שטח החתך קבוע (כמו בגליל, או בתיבה) המאמץ נשאר קבוע בכל מקום. בגוף ששטח החתך שלו שונה במקומות שונים (כמו במוט שניסרו או שייפו את היקפו), נוצר ריכוז של המאמצים: הכוח פועל על שטח חתך שגודלו משתנה (קטן) ומתקבל מאמץ גדל. התמונה מראה שלוש דוגמאות של שינוי בשטח החתך והגידול במאמץ כתוצאה מכך.
תוכן עניינים
השפעת ריכוז המאמצים
כאשר המאמץ בנקודה מסוימת יעלה על יכולת החומר להתנגד לו, החומר יקרוס וישבר או ייקרע. ריכוז מאמצים נוצר במקרים רבים סביב פגמים בחומר, חורים קטנים או סדקים. ריכוז המאמצים גורם להגדלת הפגמים והסדקים, עד לשבירה של החומר כולו.
ניתן לתאר זאת על ידי הדמיה של קווי מעבר הכוח - הקווים לארכם עובר הכוח דרך החומר. במקום בו יש חור, סדק או פגם, שטח החתך קטן יותר. קווי הכוח חייבים להצטופף בשטח קטן יותר ומתקבל יותר כוח ליחידה שטח - מאמץ גדול יותר המתרכז בנקודה מסויימת. אם המאמץ גדול יותר מזה שהחומר יכול לשאת, הוא קורס.
ריכוז מאמצים בטיפוס
ריכוז מאמצים בקשרים
ריכוז מאמצים באבני עיגון
תופעת ריכוז המאמצים באה לידי ביטוי במגע בין אבני עיגון ובין הסלע. העניין חשוב בכל אבן עיגון, אך במיוחד באבני עיגון פאסיביות (רוקים). ההנחיה הכללית היא להשתמש ברוקים כך ששטח המגע בין העגינה לבין הסלע הוא מקסימאלי. הרעיון הוא שככל ששטח המגע גדול, כך המאמץ קטן. אם השטח קטן, נאמר רוק שיושב על ארבעה זיזים קטנים של סלע, כל המאמץ יתרכז בהם והסיכוי שאחד מהם יישבר והעגינה תצא - גדול. זה נכון גם לפרנדים, טריקמים וכל עגינה אחרת.
קריעת נייר ברצועות
קריעת נייר ברצועות דומה במקצת לריכוז מאמצים בתוך קשר, אבל היא מקרה קיצוני יותר בגלל המבנה השטוח של הרצועות. המבנה גורם לכך שכל קרע קטן בשפה של רצועה עלול לגדול במהירות ולהפוך לכשל של כל הרצועה. גם כאן, הריכוז של קווי הכוח בקצה הקרע מתבטא בריכוז מאמצי המתיחה בשטח קטן, ואיזור זה נקרע. ככל שהקרע גדל, יותר קוי כוח מתרכזים בקצה הקרע ושוב, הקרע גדל.
זה דומה לכשל בגלל ריכוז מאמצים בקורה קשיחה, אבל שוב, קיצוני יותר כי הרצועה אינה קשיחה והחלק הקרוע יכול להיפתח ולהעביר את הכוח לקצה של הקרע יותר בקלות. ברצועות, בניגוד לקורות, יש הבדל במיקום הפגם ופגמים על השפה מחלישים את הרצועה הרבה יותר מחור באמצע הרצועה, למשל. חשוב להזכיר גם שרצועות מתמודדות היטב עם מאמצי מתיחה, והן משנות את צורתן כמעט ללא התנגדות תחת מאמצים אחרים: דחיסה, כפיפה ופיתול.
עןד תופעה מתרחשת במקרים שבהם הרצועה נמשכת לא לארכה אלא באופן שקצת מעוות אותה. במקרה כזה, רק חלק קטן משטח הרצועה נושא את העומס וכל המאמץ מתרכז שם. זה דומה לקריעה של פלסטר או רצועת פלנלית, רק ששם אנחנו בכוונה מתחילים מן השפה, כדי שיהיה לנו יותר קל לקרוע אותה.

בקשרים ברצועות, במיוחד קשרי חביקה כמו בקביעה הנבנית משתי רצועות שלובות זו בזו, או מרצועה וחבל (girth hitch) או רצועה וכבל. זה דומה גם בקשר הנראה בתמונה של רצועה על מוט, שנקרא קשר משקפים או לפעמים "קשר סכין", ובו הרצועה עלולה לחתוך את עצמה.
בקשר כזה, מקבלים את שתי התופעות שתוארו. קודם כל, השפה של הרצועה נשחקת תחת עומס ברצועה האחרת (או בחבל או בכבל). זה גורם להופעה של קרעים קטנים בשפת הרצועה. בהמשך, הקרעים הקטנים גדלים במהירות עד לכשל של הרצועה. בתמונה נראית רצועת דיינימה שנקרעה בקשר כזה תחת משקל גוף!
קיימת טענה מקובלת שרצועות טובולריות רגישות פחות לקריעת נייר מרצועות שטוחות. זה בגלל שלרצועות טובולריות אין ממש שפה. הן שטוחות בכיוון הזה רק מתוך מקריות, ולמעשה אפשר להרחיק כל קרע קטן מן השפה על ידי גלגול הרצועה, כך שלא יהיה על השפה אלא יותר כמו חור באמצע הרצועה.
קישורים חיצוניים
תרמו לדף זה: מיכה יניב, שחר קדמיאל ואחרים...