ריכוז מאמצים

סוגי מאמצים

מאמץ (stress) נמדד ביחידות כוח ליחידת שטח, למשל בניוטון (או קילוניוטון או ק"ג) למילימטר מרובע (או עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): cm^2 או עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): m^2 ).

מאמץ מתיחה ודחיסה למשל הוא עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \sigma=\frac{F}{A}

כאשר: עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \sigma - ערך המאמץ, עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): F - ערך הכוח הפועל, עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): A - שטח חתך הגוף.

ניתן לראות שככל שהכוח הפועל על הגוף גדל, גדל גם המאמץ ואילו ככל ששטח החתך גדל, המאמץ קטן. הגדרת מאמץ היא כוח ליחידת שטח (כמו לחץ). ריכוז מאמצים נוצר כאשר כוח פועל על שטח שגודלו הולך וקטן (ומכאן שהמאמץ הולך וגדל).

כאשר המאמץ בנקודה מסוימת יעלה על יכולת החומר להתנגד לו, החומר יקרוס, ישבר או ייווצר בו חור (כך יוצר מהדק סיכות חור בנייר).

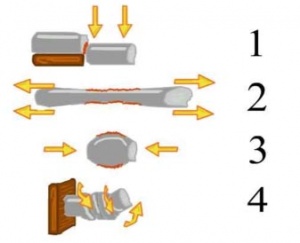
סוגי המאמצים: קיימים 3 סוגים של מאמצים בתוך חומר: מתיחה (שאיפה של חלקיקים להתרחק אחד מהשני), לחיצה (שאיפה של חלקיקים להתקרב אחד לשני) וגזירה (שאיפה של חלקיקים להיפרד זה מזה על המישור הניצב לקו המקשר ביניהם). שאר המאמצים הם מקרים פרטיים של מאמצים אלו או שילוב של מאמצים אלה.

1 - גזירה

2 - מתיחה

3 - דחיסה

4 - פיתול

(האיור מתוך עבודת סיום קורס מדריכי טיפוס של אבישי חכים).

עקומת מאמץ-מעוות

עקומת מאמץ-מעוות

בעת הפעלת כוח על גוף, מידותיו משתנות (גם אם לפעמים במידה קטנה, כזו שקשה להבחין בה). שינוי הגודל נקרא מעוות. את המעוות מחשבים באופן יחסי: אם נחלק את האורך החדש של הגוף באורך המקורי, נקבל את המעוות (strain).

כאשר: עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): E - מודול האלסטיות עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \varepsilon - מעוות עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \sigma - מאמץ

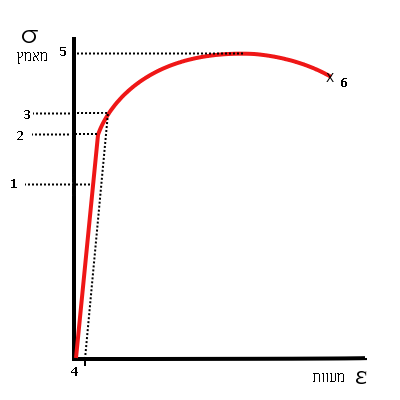
עקומת מאמץ-מעוות היא העקומה הנוצרת משרטוט המאמץ הפועל על החומר והמעוות הנוצר ממנו. הצורה הכללית של העקומה מאמץ-מעוות היא ליניארית בתחילתה, כלומר שמתקיים יחס קבוע בין הגידול במאמץ לבין הגידול במעוות. תחום המאמצים בהם היחס קבוע נקרא התחום האלסטי. בתחום זה החומר "זוכר" את צורתו וחוזר אליה לאחר הסרת המאמץ המופעל עליו. בתחום האלסטי נוצרים בחומר רק מעוותים אלסטיים, כלומר, כאלה הנעלמים עם הסרת הכוח הפועל.

היחס בין מאמץ למעוות בתחום האלסטי נקרא מודול האלסטיות של החומר. גודל זה ידוע גם כמודול יאנג (Young's modulus). על שמו של תומס יאנג. במודלים פשוטים של חוזק, גודל זה קבוע, אך במודלים מורכבים יותר ובחומרים שונים הקשר בין מאמץ למעוות חדל להיות לינארי. מודול האלסטיות המבטא את הגמישות של החומר.

עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): E =\frac{\sigma}{\varepsilon} או עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \sigma = E*\varepsilon

במאמץ גדול יותר, החומר עובר לתחום הפלסטי. באותה נקודה, הנקראת נקודת הכניעה (או גבול הכניעה) הגרף מאבד את הלינאריות שלו. העקומה משתנה ונהיית מורכבת יותר ולא לינארית.

כאמור, כל שינוי של מידות הגוף בתחום החלק הלינארי הוא הפיך, כלומר עם הסרת העומס תחזור הגאומטריה של הקורה לקדמותה (כמו חבל בעומס נמוך). אבל מעוות שמעבר לתחום הלינארי הוא לא הפיך, כלומר גם כאשר יוסר העומס, תשמר הגיאומטריה החדשה. בתחום הפלסטי, בעת שחרור המאמץ החומר לא חוזר למצבו ההתחלתי, ונותרים בו מעוותים פלסטיים.

מאמץ כניעה: המאמץ בו עובר החומר מהתחום האלסטי לתחום הפלסטי.

נקודת השבירה: המאמץ בו מתרחש כשל של החומר (קריעה, שבירה).

'הביטוי הזה ידוע גם כחוק הוק.

ריכוז מאמצים

קריעת נייר ברצועות

---

תרמו לדף זה: מיכה יניב ואחרים...