ריכוז מאמצים

סוגי מאמצים

מאמץ (stress) נמדד ביחידות כוח ליחידת שטח, למשל בניוטון (או קילוניוטון או ק"ג) למילימטר מרובע (או עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): cm^2 או עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): m^2 .

מאמץ מתיחה ודחיסה למשל הוא עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \ \sigma = \frac{F}{A} כאשר: עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \ \sigma - ערך המאמץ, עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): F - ערך הכוח הפועל, עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): A - שטח חתך הגוף.

ניתן לראות שככל שהכוח הפועל על הגוף גדל, גדל גם המאמץ ואילו ככל ששטח החתך גדל, המאמץ קטן. הגדרת מאמץ היא כוח ליחידת שטח (כמו לחץ). ריכוז מאמצים נוצר כאשר כוח פועל על שטח שגודלו הולך וקטן (ומכאן שהמאמץ הולך וגדל).

כאשר המאמץ בנקודה מסוימת יעלה על יכולת החומר להתנגד לו, החומר יקרוס, ישבר או ייווצר בו חור (כך יוצר מהדק סיכות חור בנייר).

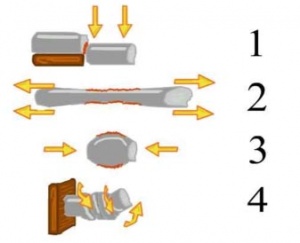
סוגי המאמצים: קיימים 3 סוגים של מאמצים בתוך חומר: מתיחה (שאיפה של חלקיקים להתרחק אחד מהשני), לחיצה (שאיפה של חלקיקים להתקרב אחד לשני) וגזירה (שאיפה של חלקיקים להיפרד זה מזה על המישור הניצב לקו המקשר ביניהם). שאר המאמצים הם מקרים פרטיים של מאמצים אלו או שילוב של מאמצים אלה. 1 - גזירה

2 - מתיחה

3 - דחיסה

4 - פיתול

(האיור מתוך עבודת סיום קורס מדריכי טיפוס של אבישי חכים).

עקומת מאמץ-מעוות=

קובץ:Stress v strain 2h.png

עקומת מאמץ-מעוות

בעת הפעלת כוח על גוף, מידותיו משתנות (גם אם לפעמים במידה קטנה, אשר קשה לראותה בעין). שינוי הגודל נקרא מעוות. אם נחלק את האורך החדש של הגוף באורך המקורי, נקבל גודל חדש - מעוות יחסי (strain). עקומת מאמץ-מעוות היא העקומה הנוצרת משרטוט המאמץ הפועל בדגם עבור כל ערך של עיבור. הצורה הכללית של העקומה מאמץ-מעוות היא לינארית בתחילתה, באזור בו מתקיים חוק הוקואילו לאחר מכן משתנה ונהיית מורכבת יותר (ולא לינארית). הנקודה בה הגרף מאבד את הלינאריות שלו נקראת נקודת הכניעה (או גבול הכניעה). כל שינוי של מידות הגוף בתחום החלק הלינארי הוא הפיך, כלומר עם הסרת העומס תחזור הגאומטריה של הקורה לקדמותה (כמו חבל בעומס נמוך). אבל מעוות שמעבר לתחום הלינארי הוא לא הפיך, כלומר גם כאשר יוסר העומס, תשמר הגאומטריה החדשה.

ריכוז מאמצים

קריעת נייר ברצועות

---

תרמו לדף זה: מיכה יניב ואחרים...