דינאמיקה של נפילות

תיאור התהליכים המתרחשים בזמן נפילה. המאמצים והכוחות המופעלים על הנופל, על החבל, על העגינות ומכשיר החיכוך.

כמה הגדרות

נפילת הובלה

נפילה בהובלה במקרה בו המטפס נמצא מעל העגינה האחרונה שלו. הנפילה נחשבת חמורה יותר ככל שהכוח המתפתח במהלך בלימת הנפילה גדול יותר.

כוח בלימה

הכוח המקסימאלי המתפתח בזמן בלימת נפילה.

מרחק בלימה

המרחק עליו מתבצעת הבלימה. בבלימת נפילה מרחק הבלימה הוא מידת התארכות החבל בזמן בלימת הנפילה.

אלאסטיות

מתיחות, תכונתו של גוף לשנות אורך כאשר מפעילים כוח.

מודול החבל

היחס בין הכוח המופעל לבין מידת ההתארכות.

מקדם נפילה

היחס בין אורך הנפילה לבין אורך החבל המשתתף בבלימה. מקדם הנפילה משמש מדד לחומרת הנפילה. מקדם הנפילה הולך כמו כוח הבלימה.

התארכות

היחס בין האורך המקורי לאורך לאחר מתיחה.

מבוא

בזמן טיפוס מתרחשות נפילות בהם המטפס ניתק מהקיר ומערכת האבטחה (חבל, עיגון, רתמה, מאבטח...) בולמת את נפילתו. בזמן הנפילה ובזמן בלימתה מופעלים על מערכת האבטחה כוחות פיסיקליים ונספגת בה אנרגיית הנפילה.

הבנת ה"דינמיקה של הנפילה" תאפשר לנו להעריך איזו נפילה "חמורה" יותר ואיזו "חמורה" פחות, ולהיערך מראש (על ידי בחירת ציוד מתאים, מיקום נכון של העוגנים וכו') על מנת להקטין את חומרת הנפילה.

חלקי מערכת האבטחה

נתחיל את הדיון בדינמיקה של הנפילה בזיהוי חלקי מערכת האבטחה ופעולתם בזמן הנפילה. באופן סכמתי נחלק את מערכת האבטחה לארבעה חלקים עיקריים:

1. המטפס – בזמן נפילה המטפס יורד מגובה מסוים לגובה נמוך יותר ותוך כדי כך מאיץ וצובר מהירות, בזמן בלימת הנפילה מאיט המטפס עד לבלימה מלאה על ידי מערכת האבטחה. במילים אחרות האנרגיה הפוטנציאלית של המטפס הופכת לאנרגיה קינטית וזו בתורה נספגת ומפוזרת על ידי מערכת האבטחה. מאחר ואנרגיה פוטנציאלית תלויה בגובה ובמסה, ברור שאורך הנפילה ומשקלו של הנופל הם גורמים משמעותיים לחומרת הנפילה.
 באופן טבעי נשאף שהכוח המופעל על המטפס בזמן בלימת הנפילה יהיה קטן ככל האפשר. כוחות גדולים שיפעלו על המטפס עלולים לגרות לפגיעה פיזיולוגית בו, או לכשל של הציוד שעליו (רתמה).

2. נקודת העיגון – נקודה זו חשובה לענייננו מאחר שבהזנחת חיכוך וללא אבטחה דינאמית, יופעל על נקודה זו (אם מזניחים את החיכוך) כוח כפול מהכוח שיופעל על חלקי המערכת האחרים (הסבר בהמשך) ולפיכך נקודת העיגון נמצאת בסיכון גבוהה לכשל ציוד.

3. חבל – החבל הוא האלמנט במערכת שסופג את מרבית אנרגית הנפילה. מרבית האנרגיה הקינטית מומרת לחום על ידי חיכוך החבל בגורמים חיצוניים (טבעת העיגון, אמצעי האבטחה, חיכוך עם הקיר) וחיכוך פנימי בין סיבי החבל. השאר מומרת לאנרגיה אלאסטית על ידי התארכות החבל בזמן הבלימה. הדרך המדוייקת שבה נספגת האנרגיה על ידי החבל בזמן התארכותו היא מחוץ להיקף של דיון זה, ונזכיר רק שמידת האלסטיות של החבל ואורך החבל שסופג את אנרגיית הנפילה משמעותיים מאד לחומרת הנפילה:

ככל שהחבל אלסטי יותר הוא יתארך יותר בקלות, וככל שהקטע שסופג את הנפילה יהיה ארוך יותר הוא יוכל להימתח יותר, והבלימה תהיה "רכה" יותר (חישבו על נפילה על כבל פלדה לעומת חבל בנג'י).

4. נקודת האבטוח – נקודת האבטוח כוללת את אביזר החיכוך, המאבטח והציוד הנלווה. למרות שלאביזר החיכוך ולמאבטח יכולה להיות השפעה עצומה על הפחתת הכוח הפועל במערכת בזמן בלימת הנפילה, לצורך דיון זה נניח שעצירת החבל בנקודת האבטוח היא מיידית.

הכוח המופעל בזמן נפילה

בהזנחת השפעות החיכוך, הופך הכוח המופעל בזמן הנפילה לתלוי בשלושה גורמים: מקדם הנפילה, משקל המטפס וסוג החבל.

דוגמאות לעומסים הפועלים בנפילות שונות

הכוח המכסימלי הפועל על המטפס ( Kg )	פרטי הנפילה	סוג החבל
1800~	מטפס במשקל 80 קילו, מקדם נפילה 2	סטטי
900~	מטפס במשקל 80 קילו, מקדם נפילה 2	דינמי
600~	מטפס במשקל 80 קילו, מקדם נפילה1.1	דינמי
350~	מטפס במשקל 80 קילו, מקדם נפילה0.25	דינמי

יש לשים לב לכך שמאחר ובנקודת העגינה האחרונה מופעל הכוח בשני הכיוונים, לכיוון המטפס ולכיוון המאבטח, יכול הכוח על העגינה להגיעה לעד פי שניים מהכוח המופעל על המטפס.

אורך הנפילה

בחלק הקודם ראינו שהכוח הפועל במערכת תלוי במקדם הנפילה ולא באורך הנפילה. עם זאת, אין זה נכון שנפילות בעלות אותו מקדם נפילה "חמורות" באותה מידה כאשר באחת אורך הנפילה גדול משמעותית מאשר באחרת. אם נתעלם מסכנת הפגיעה במדפים או בליטות סלע, כאשר אורך הנפילה גדול יותר האנרגיה הפוטנציאלית של המטפס, שנספגת על ידי החבל ועבודת החיכוך במערכת, גדולה יותר ככול שאורך הנפילה גדול יותר. במילים אחרות, למרות שהכוח המקסימלי תלוי במקדם הנפילה ולא באורך הנפילה. בנפילות ארוכות יופעל הכוח במשך זמן רב יותר מאשר בנפילות קצרות (או לאורך דרך ארוכה יותר).

ספיגת האנרגיה בחבל בזמן בלימת הנפילה משפיעה עליו לרעה בשתי דרכים:

התארכות החבל והפחתת היכולות הדינמיות שלו – בזמן ספיגת האנרגיה של הנפילה החבל מתארך ומאבד מהתכונות האלסטיות שלו כך שבנפילה הבאה יכולתו לספוג אנרגיה קטנה יותר. ידוע שאם נותנים לחבל "לנוח" אחרי שספג נפילה הוא "מתכווץ" חזרה (גם אם לא לגמרי) ובמידה מסוימת מחזיר לעצמו לפחות חלק מהתכונות האלסטיות שלו.
מבחינה זו משולה נפילה ארוכה למספר נפילות קצרות ללא כל מנוחה בינהן, ולכן היא "חמורה" בהרבה מנפילה קצרה באותו מקדם.

חימום – בזמן בלימת הנפילה האנרגיה הפוטנציאלית שהפכה לאנרגית הימתחות של החבל, הופכת לחום שנוצר כתוצאה מעבודת חיכוך (אחרת היינו ממשיכים להתנדנד מעלה ומטה על החבל לנצח). החום נוצר כתוצאה מחיכוך בגורמים חיצוניים כמו טבעות או הסלע, וגם כתוצאה מחיכוך בתוך החבל בין הסיבים השונים ובין הליבה למעטפת, והוא מפוזר בין חלקי המערכת ומשם אל האוויר, לחום השפעה מזיקה על החבל והוא עלול לגרום לו לדפורמציות – התכה של סיבי החבל והתקשות בצורה אחרת (לא סיבית) או אפילו בהמסה מלאה.
 כאמור, בנפילה ארוכה יותר האנרגיה הפוטנציאלית המתפזרת בחבל גדולה יותר, ולכן החום שנוצר במערכת גדול יותר. מבחינה זו נפילה ארוכה היא חמורה יותר מנפילה קצרה באותו מקדם.

השפעת התופעות שהוסברו כאן היא משמעותית ביותר, ולכן חבל שספג נפילה ארוכה צריך להיפסל גם אם המקדם אינו גבוהה במיוחד.

הכוח המופעל על המטפס בנפילה כפונקציה של הזמן בנפילה ארוכה ובנפילה קצרה:

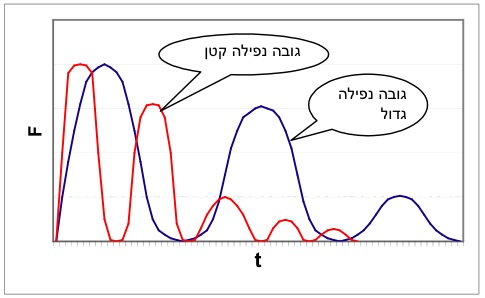
סיכום ביניים

מקדם הנפילה מוגדר כיחס בין אורך הנפילה לאורך החבל שסופג אותה, והוא מדד חשוב להערכת הכוח הפועל במערכת בזמן נפילה, אם כי קשה להעריך את גודל הכוח וקל יותר להשוות חומרת שתי נפילות.

ככל שמקדם הנפילה גדול יותר הנפילה חמורה יותר.

בהינתן שתי נפילות בעלות מקדם זהה, הנפילה הארוכה יותר, חמורה יותר.

ככל שהחבל אלסטי יותר תיספג הנפילה טוב יותר והעומס במערכת יקטן. חובה להשתמש בחבלים דינמיים - מתיחים בטיפוס הובלה.

בהזנחת חיכוך המתיחות בחבל זהה בכל נקודה ולכן הכוח על העגינה האחרונה (בה החבל מכופף ב-180 מעלות בקרוב, יכול להגיע לעד פי שניים מהכוח הפועל על המטפס.

בהינתן שתי נפילות באותו אורך, זו שבה מרחק העגינה האחרונה מהמאבטח גדול יותר, תפעיל פחות עומס על המערכת.

כאשר מתחילים לטפס מהקרקע, מקדם נפילה 1 משמעו פגיעה בקרקע.

מכסימום מקדם הנפילה בהובלה הוא 2.

חישובים פיסיקליים בנפילת מוביל בתנאים אידיאליים

הנחות עבודה

• אין חיכוך של החבל בשום גורם אחר.

• האבטוח סטטי ולא דינמי (אין החלקת חבל באביזר החיכוך).

• החבל מעוגן בעיגון קבוע בצד האבטוח.

סימונים

עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): L – אורך החבל (1רגל=0.3מטר)

עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): W – משקל המטפס (LBS 1 ליברה =0.45ק"ג)

עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): F - הכוח המכסימלי על המוביל בנפילה

עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): K – קשיחות החבל (מוגדרת ע"י קבוע החבל ואורך החבל בו מדובר)

עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): M – מודול החבל (לכל חבל מודול משלו)

עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \delta - השינוי באורך החבל

עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \epsilon - אורכו המקורי של החבל חלקי השינוי באורך החבל

היחסים הבאים מתקיימים:

עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): F=K\delta

עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): K=\frac{M}{L}

עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): M=\frac{F}{\epsilon}

עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \epsilon=\frac{L}{\delta}

עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \delta=\frac{F}{K}

הנחה : עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): M קבוע ואינו משתנה תחת עומס.

האנרגיה הפוטנציאלית של המטפס :

עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): E_p=mg(h+\delta)=W(h+\delta)

חבל, בניגוד לקפיץ, ההנחה שעיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): K ליניארי, הינה מחמירה, שכן האנרגיה גבוהה יותר מזו שנספגת בחבל באמת (השטח מתחת לקו הישר גדול מזה שמתחת לעקומה). ואז נקבל כי:

עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): F(x)=K\delta

האנרגיה הנאגרת בקפיץ הסופג את הנפילה (החבל):

עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): E=\int_0^\delta F(x)dx=\frac{k\delta^2}{2}

עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): E_P=E

עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): W(h+\delta)\frac{k\delta^2}{2}=

עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \frac{k\delta^2}{2}-w]delta-Wh

עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \delta=\frac{W\pm\sqrt{W^2+2WKh}}{K}=\frac{W\pm W\sqrt{1+\frac{2Kh}{W}}}{K} \frac{W\pm W\sqrt{1+\frac{2Mh}{WL}}}{K}

עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): F=K\delta=W\left(1\pm\sqrt{1+\frac{2Mh}{WL}\right} ניתן להתייחס רק לשורש החיובי של המשוואה מאחר ולשורש השלילי נקבל ערך שלילי למשוואה כולה:

עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): F=W\left(1+\sqrt{1+\frac{2Mh}{WL}\right}

הכוח המכסימלי על המוביל הוא :

הכוח המכסימלי על המוביל כפונקציה של המודול, משקל המטפס ומקדם הנפילה הוא :

טבלאות כוח מכסימלי על המטפס (קג"כ)

קביעת מודול החבל מתוך נתוני היצרן:

היצרן מספק לנו בד"כ נתונים עבור נפילה סטנדרטית:

FF=1.78

W=80Kg

F – הכוח המכסימלי שיפעל בנפילה כזאת על המטפס

לדוגמא: אם היצרן מצהיר על 80 KN כוח מכסימלי אז M יהיה :

אם היצרן מצהיר על 90 KN כוח מכסימלי אז M יהיה :

מודולים של חבלי הובלה הם באזור 2,500 ק"ג ואילו של חבלים סטטיים באזור 8,500 ק"ג.

מרחקים בין עיגונים בהובלה

חלק זה ינסה לבדוק מהו הגובה הבטוח מעל העיגון האחרון אליו ניתן לטפס ללא הנחת עיגון נוסף.

לבדיקה זו נחלק את העיגונים לשני סוגים:

עיגונים בעלי חוזק גבוה (בולטים אשר מותקנים היטב, הקסים על סלינג או ) – 1800 ק"ג

עיגונים בעלי חוזק נמוך (רוקים לסוגיהם ו-camming devices) – 900 ק"ג

מאחר ואנו מניחים כי העומס על העיגון האחרון כפול מהעומס על המטפסת, נרצה כי העומס על המטפס לא יעלה על 900 ו 450 ק"ג בהתאמה. דוגמת חישוב

עיגון בעל חוזק גבוה

עומס מותר על המטפס 900 ק"ג
 לכן בהנחה שמטפס שוקל 80 ק"ג FF המותר הוא בערך 1-1.25
 מכאן שמותר לטפס מעל העיגון קצת פחות מגובהו של העיגון מעל האבטוח (יש לקחת בחשבון מתיחות אם לא רוצים להימרח על הקרקע).

עיגון בעל חוזק נמוך

עומס מותר על המטפס 450 ק"ג
 לכן בהנחה שמטפס שוקל 80 ק"ג FF המותר הוא בערך 0.25-0.3
 מכאן שמותר לטפס מעל העיגון קצת פחות משישית מגובהו של העיגון מעל האבטוח (יש לקחת בחשבון מתיחות אם לא רוצים להימרח על הקרקע).

מהירות המוביל הנופל ברגע התחלת הבלימה

נשתמש בנוסחה לחישוב נפילה חופשית

מאחר והמהירות ההתחלתית היא 0 ו- g=9.8 נקבל במטרים לשניה כי:

מהטבלה ניתן לראות בקלות כי יש להתחשב גם בגובה הנפילה בלי קשר ל- FF מאחר ובמהירויות גבוהות פגיעה בסלע (אם הנפילה אינה בשלילי חזק) עלולה להיות בלתי נעימה ואף מסוכנת.

נושאים נוספים

שני הנושאים הבאים הנם מחוץ לתחומה של עבודה זו וההתייחסות אליהם היא ערכית ולא מספרית. השפעת אבטחה דינאמית וחיכוך בטבעת העליונה (של העיגון האחרון) על הכוחות בנפילה

חיכוך בטבעת העליונה הוא גורם המשפיע על הכוחות מאחר ומתבצעת עבודה אשר יש לקחת בחשבון בחישובי האנרגיה.

גם אבטוח דינמי הוא גורם המשפיע על הכוחות מאחר וגם כאן מתבצעת עבודה (חיכוך החבל באביזר החיכוך והתרוממות המאבטח).

באופן כללי נציין כי עבודת חיכוך בטבעת העליונה תגדיל את הכוח הפועל על המטפס הנופל, ותקטין את הכוח הפועל על המאבטח (במידה גדולה יותר מאשר הגדלת הכוח על המטפס).

תנועת המאבטח גם היא מורידה מהעומס על המערכת. כאשר המאבטח מתרומם כלפי מעלה בזמן עצירת הנפילה, הרי שהוא צובר אנרגיה פוטנציאלית ואנרגיה זו אינה צריכה להיספג במערכת האבטחה, דבר שמוריד את מקדם הנפילה ואת סך האנרגיה הנספגת במערכת. בנוסף, עקב תנועת המאבטח מתבצעת יותר עבודת חיכוך בחלקי המערכת השונים. לכל הפחות ניתן להגיד שכל מטר שמתרוממם המאבטח באוויר, כאילו נפל המטפס מטר אחד פחות.

גם החלקת החבל דרך אביזר החיכוך תורמת להקטנת חומרת הנפילה. בזמן החלקת החבל באביזר החיכוך מתבצעת עבודה באביזר החיכוך (כמו גם בחלקי המערכת האחרים), בהערכה גסה, אם נניח שמחליק כחצי מטר דרך אביזר החיכוך, וכוח הבלימה הוא כ150 קג' כוח, הרי שהחלקה כזו שוות ערך להקטנת אורך הנפילה בכ1 מטר. ניתן עתה לחשב מחדש את הכוחות לקבלת הערכה טובה יותר (אם כי עדיין רק הערכה).

החישובים בעבודה זו מבוססים על עבודתו של Stephen W. Attaway שכתב לזכרם של שלושה חברים אשר נהרגו בנפילה של 259 מטר ב23 ביוני 1996 (סיפור המקרה הופיע במגזין Climbing).

---

תרמו לדף זה: מיכה יניב, דורון נצר, ארנון נצר ואחרים...