הבדלים בין גרסאות בדף "איך עובדים אמצעי חיכוך?"
| שורה 20: | שורה 20: | ||
<math>F_f=T_2\times(1-e^\alpha)</math> | <math>F_f=T_2\times(1-e^\alpha)</math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
[[תמונה: capstan1.jpg|eft|200px]] | [[תמונה: capstan1.jpg|eft|200px]] | ||
גרסה מ־06:02, 19 בדצמבר 2007
מאמר בעבודה!
אופן הפעולה של רובם המכריע של אמצעי החיכוך מודגם יפה על ידי חבל המלופף על תוף. הרעיון של אמצעי החיכוך הוא לגרום לחבל להפעיל כוח בניצב לאביזר, וכך ליצור כוח חיכוך. ככל שהחיכוך גדול יותר, כך נדרש להפעיל פחות כוח בהחזקת החבל. הדרך לעשות זאת היא ליצור "שבירה" של החבל סביב משהו: תוף, טבעת, עמוד, אמצעי חיכוך.
אותו עיקרון פועל גם לאורכו של חבל המתחכך בסלע.
תזכורת קצרה: כוח החיכוך ניתן על ידי: עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): F_f=\mu F_N . כאשר: עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \mu נקרא מקדם החיכוך והוא תכונה של שני החמרים של הגופים הבאים במגע, ו עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): F_N , הכוח הנורמלי, הוא הכוח הניצב למישור המגע בין שני הגופים.
כדי להבין את המשך המאמר אין צורך להתעמק בפיתוח המתמטי-פיזיקלי. המאותרגים מתמטית מוזמנים לקחת את הנוסחה הסופית, ולדלג על החישובים.
כדי להבין זאת נסתכל על כוח החיכוך על אלמנט אורך חבל על תוף:
בתוף מקוטר מסויים ומעלה, אין השפעה לאורך החבל המתחכך בתוף (ולכן אין השפעה לקוטר התוף), אלא לזוית שעובר החבל סביב התוף.
אם נסמן את הזוית ב עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \alpha , ואת העומס על החבל ב עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): T_2 , נקבל כי הכוח בו צריך למשוך את החבל בצד השני של התוף math>T_1</math> הוא:
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): T_2=T_1\times e^ \alpha
וכוח החיכוך הוא ההפרש בין המתיחויות בחבל בשני צידי התוף:
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): F_f=T_2\times(1-e^\alpha)
כשקטע קצר של חבל עובר על חלק של תוף עגול, ניתן לחשב בקלות את החיכוך. נניח שהקטע שנוגע בחבל הוא כלכך קצר, שהוא ישר, בקירוב. נתאר את הכוחות הפועלים עליו:
המתיחות בחבל הקרוב למשקולת, הוא המשקל, לכן: עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): T_2=w .
המתיחות אחרי התוף קטנה יותר, ומסומנת כאן עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): T_1 .
כוח החיכוך, עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): F_f
, תלוי בכוח הנורמאלי, עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): F_N
. נחשב אותו:
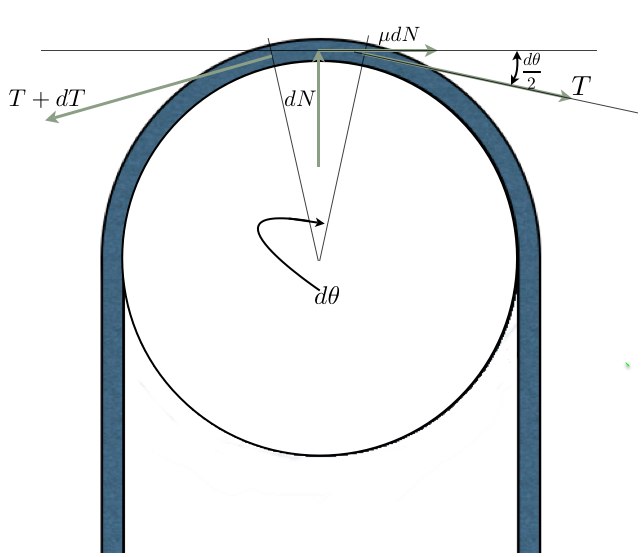כשהחבל עובר על התוף, המתיחות גדלה ב עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): dT
עם שינוי של עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): d\alpha
בזווית. נסמן את הכוח הנורמלי שמפעיל אלמנט חבל זה בעיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): dN
.
כוח החיכוך, יהיה עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): F_f=\mu F_N .
