הבדלים בין גרסאות בדף "Effective fall factor"
| שורה 1: | שורה 1: | ||
| − | {{ | + | {{LTR}} |
'''מקדם נפילה אפקטיבי''' | '''מקדם נפילה אפקטיבי''' | ||
'''Effective fall factor''' or as it is sometimes called '''real world fall factor''' is the actual [[Fall Factor]] that will determine the [[impact force]] that will develope durim=ng the breaking of a [[lead fall]]. When estimating the fall factor, the full length of the [[ropes|rope]] between the falling climber and the [[belay device]] on the belayer's [[harness]]. Since the rope is dragged over rock and through the [[binners]] of the [[runners]], the friction prev ents from the rope to elongate evenly, thus making the effective, real world fall factor to be higher aa well as the impact force. | '''Effective fall factor''' or as it is sometimes called '''real world fall factor''' is the actual [[Fall Factor]] that will determine the [[impact force]] that will develope durim=ng the breaking of a [[lead fall]]. When estimating the fall factor, the full length of the [[ropes|rope]] between the falling climber and the [[belay device]] on the belayer's [[harness]]. Since the rope is dragged over rock and through the [[binners]] of the [[runners]], the friction prev ents from the rope to elongate evenly, thus making the effective, real world fall factor to be higher aa well as the impact force. | ||
גרסה מ־07:51, 5 בספטמבר 2010
מקדם נפילה אפקטיבי Effective fall factor or as it is sometimes called real world fall factor is the actual Fall Factor that will determine the impact force that will develope durim=ng the breaking of a lead fall. When estimating the fall factor, the full length of the rope between the falling climber and the belay device on the belayer's harness. Since the rope is dragged over rock and through the binners of the runners, the friction prev ents from the rope to elongate evenly, thus making the effective, real world fall factor to be higher aa well as the impact force.
We remind that the fall factor is the ratio between the length of the fall and the length of the rope used to break it. If עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): h is the fall length, and עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): L is the length of the rope that's elongated while breaking it, we get can calculate the fall factor to be:
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): FF=\frac {h}{L}
We assume, of course, that the whole rope is elongated evenly. But is that assumption justified? In amost every conceivable lead fall, the rope passes through a few runners, and touches the rock too. The friction on the rope makes different segments of rock absorb different amounts of the kinetic energy of the fall. the meaning is that the impact force will be larger, and similar to one generaten in a higher fall factor fall.
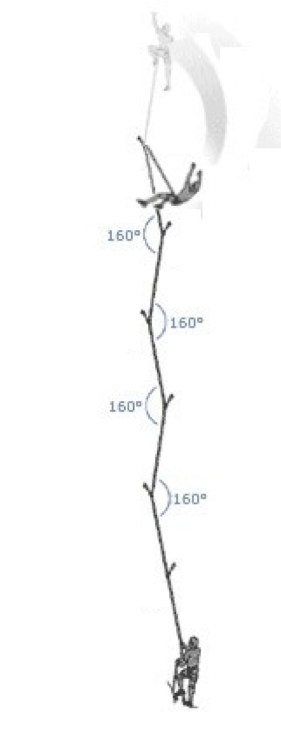
The friction of the rope passing through binners effectively devides the rope into different sections, each with a different tension. If the rope changes direction in the binner not only the leader will have more drag, but in the case of a lead fall, it separates between the segments of length of rope. the more the angle differs from 180°, the more different the tention will be between segments. In this case, the fall factor is no longer a good estimator for the impact force, since the whole length of rope is not equally elongated. A better estimate would be to use an "effective" fall factor, which will allways be larger than the theoretical one. This means the impact force will be larger, and the fall - more severe. This is especially evident by the difference between the force applied to the falling climber, and the force felt by the belayer. Ideally they should be the same, but actually, the difference is not negligible. This difference is actually the sum of friction forces in all the runners. It can be calcukated by summing up al the angles of the rope and substiting the total angle in the formula:
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): F_f=T_2(1-e^{\mu(180N-\alpha})\,\!
Where:
- עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): T_2 is the force on the falling leader
- עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \mu is the friction coefficient between rope and binner
- * עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): N is the number of binners in the system
- עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \alpha is the sum of angles
Without calculating it might seem that the friction is not signifficant, but it is. This is rigorously explained in the article about how do friction devices work? and here we'll give only a short outline:
The friction of a rope on a capstan (strangely enough, the diameter of the capstan has no effect) is determined by the angle the rope spans whyly going around the capstan. A rope hanging from a binner, for axample, will span 180°. For a rope passing through a binner, the angle can simply be calculated as עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): 180°-\alpha , עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): 180°-\alpha being the angle between the ropes on both sides of the binner.