17. מקדמי נפילה
שאלה
מקדם הנפילה, המסומן [math]\displaystyle{ ff }[/math], או באנגלית the fall factor, מוגדר בחוברות ובספרי הטיפוס השונים כיחס בין גובה הנפילה [math]\displaystyle{ h }[/math] לבין אורך החבל [math]\displaystyle{ L }[/math] שסופג את הנפילה: [math]\displaystyle{ ff=\frac {h}{L} }[/math]. לפי זה, מקדם הנפילה של מטפס שני (או של מטפס בטופ-רופ) צריך להיות אפס ([math]\displaystyle{ ff=0 }[/math]), ואם מקדם הנפילה אפס, לא הייתה צריכה להיות בכלל נפילה; החבל היה צריך להתמתח עד כדי משקל הנופל [math]\displaystyle{ g }[/math] כשהמטפס רק נשען על החבל ולא יותר. אבל התחושה בנפילת שני היא שהחבל כן נמתח, רגעית, ליותר ממשקל הנופל, משהו כמו [math]\displaystyle{ 2g }[/math] או [math]\displaystyle{ 3g }[/math], ורק אח"כ המתח בחבל פוחת ל- [math]\displaystyle{ g }[/math] ונשאר כך. לא שונה מהותית מנפילת מוביל רגילה. האין בזה סתירה?
תשובה
ההסבר יהיה הפעם קצת יותר טכני מהרגיל כי ישנם כמה מושגים (פיסיקה תיכונית בסה"כ, אבל הכרחיים) שבלעדיהם קשה להבין מה קורה לחבל ולעגינות ומה קורה לאדם הנופל (וזה לא אותו הדבר) בעת נפילה.
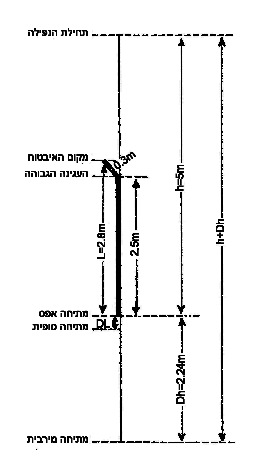
התחושה נכונה. המתח המרבי על החבל מגיע לערך גדול מ-[math]\displaystyle{ g }[/math] אף בנפילת שני (הוא [math]\displaystyle{ 2g }[/math] בחבל אלסטי לחלוטין, קצת פחות מזה בחבל מצוי). ונכון גם שמקדם הנפילה בנפילת שני הוא אפס, ובכל זאת אין פה שום סתירה. על מנת להבהיר זאת נשאל קודם שאלה יותר בסיסית: בהגדרת מקדם הנפילה [math]\displaystyle{ ff=\frac {h}{L} }[/math], מה צריך לקחת כ-[math]\displaystyle{ h }[/math] ו- [math]\displaystyle{ L }[/math]? את הערכים לפני שהחבל מתחיל להימתח, או ברגע המתיחה המרבית (הפרש גבהים [math]\displaystyle{ h+Dh }[/math] לבין אורך החבל בציור 17.1), או אולי במתיחה הסופית (אורך חבל [math]\displaystyle{ L+DL }[/math] בציור 17.1)?
ברור שלא במתיחה הסופית [math]\displaystyle{ L+DL }[/math], כי התארכות החבל הסופית [math]\displaystyle{ DL }[/math] תחת משקל [math]\displaystyle{ g }[/math] קשורה למאזן הכוח (מתח בחבל = כוח הכובד):[math]\displaystyle{ g = \frac {M \cdot DL}{L} }[/math], ולא למאזן האנרגיה, כלומר אין לה כל קשר עם גובה הנפילה [math]\displaystyle{ h }[/math] או עם אנרגית הנפילה [math]\displaystyle{ E = g\cdot\big(h+Dh\big) }[/math], שהם לב ליבו של כל עניין מקדם הנפילה [math]\displaystyle{ ff }[/math].
אשר לשתי האפשרויות הנוספות (לפני המתיחה או במתיחה מרבית), שתיהן 'כשרות' ואפשר לבחור בכל אחת מן השתים כרצוננו. במלים אחרות - זה רק עניין של הסכם, וההסכם הוא ש-[math]\displaystyle{ h }[/math] ו- [math]\displaystyle{ L }[/math] שניהם נמדדים לפני המתיחה.
כך הם מופיעים בהגדרת מקדם הנפילה, וכך מופיע ה [math]\displaystyle{ L }[/math] בהגדרת המודול [math]\displaystyle{ M }[/math] של החבל: [math]\displaystyle{ M = \frac {g \cdot L}{DL} }[/math].
המודול הזה, [math]\displaystyle{ M }[/math], מהווה מידה לקשיחות החבל ואפשר לפרשו: באיזה כוח היה צריך למתוח את החבל כדי להכפיל את אורכו, בהנחה שהחבל נשאר בתחום האלסטי. (הערה למי שקצת מתמצא: לא, זה לא מודול יאנג, אבל דומה). ערכים אופייניים למודול [math]\displaystyle{ M }[/math] בחבלי טיפוס מובאים בטבלה 17.1 (ראה גם טבלה 4.1 בפרק על גלישה בשני חבלים).
| דינאמי | סטאטי | סופרסטאטי |
| M=1000 | M=3500 | M=5000 |
נשמעת לעתים ביקורת האומרת שצריך היה להגדיר את מקדם הנפילה דווקא כ- [math]\displaystyle{ \frac {\big(h+Dh\big)}{L} }[/math], גם מכיוון שהוא הגודל המשמעותי מבחינת מאזן האנרגיה, וגם כי החישובים היו אז נעשים יותר פשוטים. שני הטיעונים האלה נכונים, אבל מאידך קשה ביותר להעריך את הגודל הזה אפילו אם ידוע מודול החבל [math]\displaystyle{ M }[/math]. ולהעריך גודל זה מהר ותוך כדי הובלה היא משימה לגמרי בלתי מציאותית. אילו בחרו בגודל הזה: [math]\displaystyle{ \frac {\big(h+Dh\big)}{L} }[/math] במקום מקדם הנפילה המקובל [math]\displaystyle{ ff=\frac {h}{L} }[/math] היה בידינו מונח שהוא בעל יותר משמעות פיסיקאלית אבל חסר תועלת לחלוטין. לכן, עבור המטפס בשטח, הועדף להגדיר את מקדם הנפילה [math]\displaystyle{ ff }[/math] כמו שהוגדר, גודל שקל להעריך אותו מהר.
כמה דוגמאות: מקדם הנפילה המרבי שאפשר להגיע אליו (ללא קוריוזים ומקרים יוצאי-דופן) הוא [math]\displaystyle{ ff=2 }[/math]. מקדם הנפילה בנפילת שני או בטופ-רופ, כפי שמצוין גם בשאלה, הוא [math]\displaystyle{ ff=0 }[/math], ומקדם הנפילה בנפילת UIAA סטנדרטית (ציורים [[ציור 9.1 בפרק על פסילה של חבל הובלה ו- 17.1) הוא [math]\displaystyle{ ff=1.79 }[/math]. בניגוד לדוגמאות האלה, הגודל [math]\displaystyle{ (h+Dh) / L }[/math], היותר משמעותי מבחינה פיסיקאלית אבל גם היותר קשה להערכה, יכול להגיע לערכים גדולים מ- 2 (2.59 בנפילת UIAA סטנדרטית, למשל), ובנפילת שני גודל זה אינו אפס אלא 0.8. וזה עונה על החלק הראשון של השאלה; התחושה שבמצב של [math]\displaystyle{ ff=0 }[/math] לא צריכה בכלל להיות נפילה אלא רק 'יושבים על החבל' היא תחושה נכונה, אבל לא לגבי מקדם הנפילה המקובל [math]\displaystyle{ ff=\frac {h}{L} }[/math] אלא לגבי הגודל המשמעותי מבחינה פיסיקאלית [math]\displaystyle{ \frac {\big(h+Dh\big)}{L} }[/math] אשר, כאמור, אינו מתאפס בנפילת שני.
באשר למאזן האנרגיה, נתחיל בשתי דוגמאות פשוטות:
דוגמה ראשונה. פטיש שמשקלו 4 ק"ג ([math]\displaystyle{ g=4kg }[/math]) נופל מגובה 50 ס"מ ([math]\displaystyle{ h=50cm }[/math]) על מסמר, אשר חודר 2 מ"מ ([math]\displaystyle{ Dh = 2mm }[/math]) לתוך קרש. מה הכוח [math]\displaystyle{ K }[/math] על המסמר?
פתרון: האנרגיה שנצברת מתחילת הנפילה ועד לעצירתה היא:
אותה אנרגיה E נבלעת בזמן הבלימה (בעת חדירת המסמר):
כאשר a תאוצת הבלימה. ולכן:
הכוח הכולל הוא סכום משקל המנוחה [math]\displaystyle{ mg }[/math] וכוח הבלימה [math]\displaystyle{ ma- }[/math]:
כלומר קצת יותר מטונה אחת:
דוגמה שניה. אותו פטיש, במשקל 4 ק"ג, נופל מאותו הגובה, של 50 ס"מ על מקל אנכי, אשר חודר 50 ס"מ בתוך חול רך (במקרה הזה: [math]\displaystyle{ g = 4kg; h = 50cm; Dh = 2mm }[/math]). מה הכוח [math]\displaystyle{ K }[/math] על המקל?
באותה שיטה מקבלים הפעם רק:
ללמדנו שהכוח [math]\displaystyle{ K }[/math] תלוי תלות חזקה מאוד בעומק הבלימה [math]\displaystyle{ Dh }[/math]: ככל שקצר [math]\displaystyle{ Dh }[/math], כך גדול הכוח [math]\displaystyle{ K }[/math].
ומדוע היו אלה דוגמאות 'פשוטות'? כי הנחנו שכוח הבלימה [math]\displaystyle{ K }[/math] קבוע במשך זמן הבלימה. לא כן בחבל טיפוס (נניח לשם פשטות אלסטי לחלוטין) שבו הכוח הולך וגדל תוך כדי בלימה ומגיע לערכו המרבי בעצירה הרגעית בשיא המתיחה, כשהאנרגיה שנבלעה היא:
אנרגיה זו שווה בדיוק לאנרגיה הפוטנציאלית של הנפילה:
שכן בנקודת המתיחה המירבית המהירות מתאפסת ואין צורך לקחת בחשבון גם את האנרגיה הקינטית. אם נשווה ביניהן, נציב [math]\displaystyle{ KL / M }[/math] במקום[math]\displaystyle{ Dh }[/math], ונציב [math]\displaystyle{ ff }[/math] במקום [math]\displaystyle{ h / L }[/math] , נקבל את משואת הבלימה (תלות הכוח [math]\displaystyle{ K }[/math] בכוח [math]\displaystyle{ ff\cdot M }[/math]):
[math]\displaystyle{ \frac {1}{2}\big(\frac {K}{g}\big)^2 - \big(\frac {K}{g}) = \big(\frac {ff\cdot M}{g}\big) }[/math]
זהירות! נוסחה אחרונה זו רשומה בצורה שגויה בחוברת המפורסמת והנפוצה מאוד של אדלריד.
קצת פרשנות: [math]\displaystyle{ K }[/math] הוא הכוח המירבי (the impact force), ו-[math]\displaystyle{ ff\cdot M }[/math] הוא כוח המתיחה שיתקבל בחבל, אם יימתח בדיוק באורך [math]\displaystyle{ h }[/math]. במשוואת הבלימה שני הכוחות אלה מבוטאים לא ביחידות של קילוגרמים או ניוטונים, אלא ביחס ל-[math]\displaystyle{ g }[/math], למשל [math]\displaystyle{ 3g }[/math], [math]\displaystyle{ 10g }[/math] וכו'. משואת הבלימה אומרת בסה"כ שאם ידוע אחד הכוחות האלה, אפשר לפיה לחשב גם את השני. התלות בין שני הכוחות האלה מוצג בצורה גראפית בציור 17.2, ורואים שה [math]\displaystyle{ ff\cdot M }[/math] הגבולי מבחינה בטיחותית הוא כ-[math]\displaystyle{ 40g }[/math]. כדאי לזכור שהכוח [math]\displaystyle{ ff\cdot M }[/math] והכוח [math]\displaystyle{ K }[/math] לבדם, אינם מהווים קנה-מידה שלם לחומרתה של הנפילה, שכן משך הזמן שהכוח פועל לא נלקח בחשבון (ראה גם ציור 9.2 בפרק על פסילה של חבל הובלה). עוד כמה דברים מעניינים שרואים ממשואת הבלימה ומציור 17.2:
1. [math]\displaystyle{ ff }[/math] ו-[math]\displaystyle{ M }[/math] באים רק ביחד ורק כמכפלה [math]\displaystyle{ ff\cdot M }[/math]. זה אומר שמקדם נפילה יותר קטן וחבל יותר דינאמי (או מקדם נפילה יותר גדול וחבל יותר סטאטי) שקולים זה כנגד זה, ורק המכפלה [math]\displaystyle{ ff\cdot M }[/math] היא שקובעת.
2. גובה הנפילה [math]\displaystyle{ h }[/math] אינו מופיע במפורש במשוואת הבלימה, אלא רק באופן סמוי בתוך [math]\displaystyle{ ff\cdot M }[/math]. יוצא מזה שכוח הבלימה [math]\displaystyle{ K }[/math] אינו תלוי ישירות בגובה הנפילה [math]\displaystyle{ h }[/math]. שתי נפילות בעלות אותו מקדם נפילה [math]\displaystyle{ ff }[/math], אחת מגובה 5 מ' ואחת מגובה 30 מ', למשל, מביאות לאותו כוח בלימה [math]\displaystyle{ K }[/math] בשני המקרים, ורק משך הזמן של פעולתו, כפי שאנו יודעים, שונה. (השווה עקומות ב' וה' בציור ציור 9.2 שהוזכר כבר).

3. יש להבדיל בין חומרת הנפילה לגבי החבל והעגינות, שאז מה שקובע הוא ה- [math]\displaystyle{ K }[/math] עצמו כפי שנמדד ביחידות של קילוגרמים או ניוטונים, לבין חומרת הנפילה לגבי האדם שנופל, שאז מה שקובע זה התאוצה, או [math]\displaystyle{ K/g }[/math], כלומר כוח הבלימה ביחס ל- [math]\displaystyle{ g }[/math]. מכת הבלימה המרבית שאדם מסוגל לשאת מבלי להזיק לאיברים הפנימיים נע בין [math]\displaystyle{ 10g }[/math] ל- [math]\displaystyle{ 15g }[/math] בהתאם למשך הזמן שכוח זה פועל. אדם כבד יחסית, נניח בעל משקל של [math]\displaystyle{ g = 90kg }[/math], הנופל על חבל דינאמי עם מקדם נפילה [math]\displaystyle{ ff=1.79 }[/math] יקבל מכת בלימה שמחושבת לפי הנוסחה שלנו כ-[math]\displaystyle{ K = 7.4g }[/math]; נפילה חזקה אבל נסבלת. אותה נפילה על חבל סופרסטאטי הייתה גורמת למכת בלימה של [math]\displaystyle{ K = 15g }[/math], וזה כבר בלתי נסבל. אותן שתי נפילות, ובאותם תנאים, אבל של אדם קל, נניח בעל משקל של [math]\displaystyle{ g = 50kg }[/math], מביאות להתארכות [math]\displaystyle{ Dh }[/math] פחותה, כלומר לנחיתה פחות רכה, ולכן מהוות נפילות יותר חמורות, דהיינו [math]\displaystyle{ 9.5g }[/math] ו- [math]\displaystyle{ 20g }[/math] בהתאמה. ערכים אלה כלולים בטבלה 17.2.
| K בחבל דינאמי | 7.4g | 9.5g |
| K בחבל סטאטי | 13g | 17g |
| K בחבל סופרבסטאטי | 15g | 20g |
רואים עוד מטבלה 17.2 שמסוכן לקבל נפילה של [math]\displaystyle{ ff=1.79 }[/math] על חבל שאינו דינאמי, שכוח הבלימה בחבל סופרסטאטי הוא בערך כפליים מכוח הבלימה בחבל דינאמי, ושמשקל [math]\displaystyle{ g }[/math] נמוך מחמיר את הנפילה לגבי הנופל (לא לגבי החבל והעגינות, כמובן).
4. ומה לעשות מכל זה מבחינה מעשית? ברור שאי אפשר להתחיל לחשב [math]\displaystyle{ K }[/math]-ים תוך כדי הובלה, אבל להעריך את מקדם הנפילה [math]\displaystyle{ ff }[/math] בהחלט אפשר, לפחות בצורה מקורבת, ואם הופכים את זה להרגל - הערכה מקורבת זו היא פשוטה, מידית, ושוטפת. מכאן שדי לזכור את הכלל המובא לעיל: ש [math]\displaystyle{ ff\cdot M }[/math] לא צריך לעלות על [math]\displaystyle{ 40g }[/math]. מטפס שמשקלו, למשל, [math]\displaystyle{ g=70kg }[/math], המשתמש בחבל הובלה בעל מודול [math]\displaystyle{ M =2000kg }[/math] יודע עוד לפני ההובלה שה- [math]\displaystyle{ ff }[/math] הגבולי שלו הוא: [math]\displaystyle{ 40 x 70 / 2,000 = 1.4 }[/math] ומשתדל לא לעבור אותו. זה רק עניין של הרגל.
5. מתקבל מהנוסחה שלנו שבנפילת שני (או בטופ-רופ), כלומר כשידוע כי [math]\displaystyle{ ff=0 }[/math], הכוח [math]\displaystyle{ K }[/math] הוא תמיד [math]\displaystyle{ 2g }[/math] (ראה גם ציור 17.2) ולא חשוב מה אורך החבל או מה קשיחותו. כבר לא צריך להפתיע אותנו שעם ערך קבוע של [math]\displaystyle{ ff }[/math], כלומר [math]\displaystyle{ ff=0 }[/math] מתקבל ערך קבוע של [math]\displaystyle{ K }[/math]. אבל זה גם עונה על החלק השני של השאלה: מקדם הנפילה המקובל [math]\displaystyle{ ff }[/math] יכול להיות אפס, אבל זה לא אומר ש [math]\displaystyle{ K=0 }[/math], אלא, כאמור, [math]\displaystyle{ K = 2g }[/math] בחבל אלסטי לחלוטין, וקצת פחות מזה בחבל מצוי, מה שבהחלט תואם את התחושה בנפילת שני.
6. כולם יודעים שעבור טופ-רופ עדיף להשתמש בחבל סטאטי מאשר בחבל דינאמי. עכשיו גם ברור מדוע: הכוח המירבי בנפילה, [math]\displaystyle{ K }[/math], ממילא אותו הדבר ([math]\displaystyle{ K = 2g }[/math]), אז לפחות שיפעל למרחק אנכי קצר ככל האפשר (בחבל סטאטי המתיחה [math]\displaystyle{ Dh }[/math] יותר קטנה) ולכן גם למשך זמן יותר קצר.
ולסיכום, טפס בזהירות ושמור על האיברים הפנימיים שלך; לא כדאי לקרוע אותם מה-'שאסי' ע"י [math]\displaystyle{ K }[/math] גדול מדי או ממושך מדי.
קריאה נוספת
- מקדם נפילה
- דינאמיקה של נפילות
- מקדם נפילה אפקטיבי
- כוח בלימה
- אבטחה דינאמית
- אבטחה דינאמית למתקדמים
- כוחות בבלימת נפילה
המשך לפרק הבא...
חזור לתוכן העניינים...
תרמו לדף זה: אנדריאה ענתי, מיכה יניב ואחרים...