?How do friction devices work
The basic principle for most friction devices can be demonstrated by a rope wrapped around a capstan. The whole purpose of a friction device is to make the rope push into the surface of the device, thus generating friction. The more friction, the easier it is for the belayer to hold the rope and arrest a fall. The way to do that is to supply friction around something: a capstan, a carabiner, a pole, a belay device.
The same principle applies along a rope dragged over rock.
תוכן עניינים
A reminder about friction and a simple calculation
A short reminder: friction is a force, and it can be calculated as: עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): F_f=\mu F_N . Where: עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \mu is called the friction coefficient and is a trait of the two materials touching and being dragged against each other, and עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): F_N , the Normal force, is the force that's perpendicular to the surface of contact between the two bodies.
In order to understand the rest, there no real need to follow all the mathematical-physical stuff. If you feel you're mathematically challenged, you can just take the final formula and skip directly to the examples section.
Let us consider the friction for a length element of a rope over a capstan.
When a short piece of rope is passing on a capstan, the friction for that length element can be easily calculated by using the basic definition of friction force. We assume that the piece of rope is so short, that it's approximately straight. The illustration describes the forces on that piece of rope:
The normal force עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): F_N , can be calculated be summing the two components of the rope tension to the עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): T directed towards the center of the capstan. We call this component עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): T_y , and it is equal to:
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): T_y=\mu T\sin\frac{\alpha}{2}
Therefore, the friction force is:
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): F_f=\mu F_N=2 \mu T_y\,\!
or, substituting עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): F_N :
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): F_f=2\mu T \sin\frac{\alpha}{2}
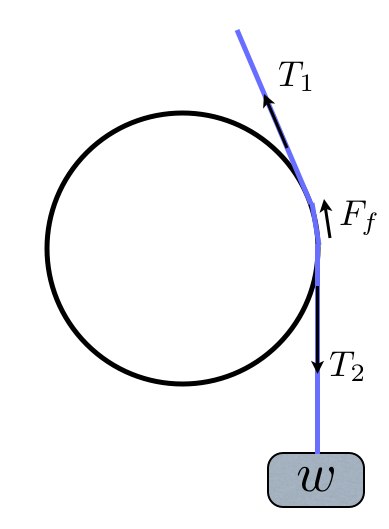
The friction force works against the sliding of the rope on the capstan, and in fact, the tensions on both sides of the capstan are not the same. The following illustration is more realistic:
The Tension on the rope tied to the load is the load itself. We call that עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): T_2 and we can write: therefore:
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): T_2=w .
The tension on the other side of the capstan is smaller, and is called here simply עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): T_1 .
The friction force, עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): F_f , is proportional to the normal force, עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): F_N , which we've already found.
A little more complicated calculation.
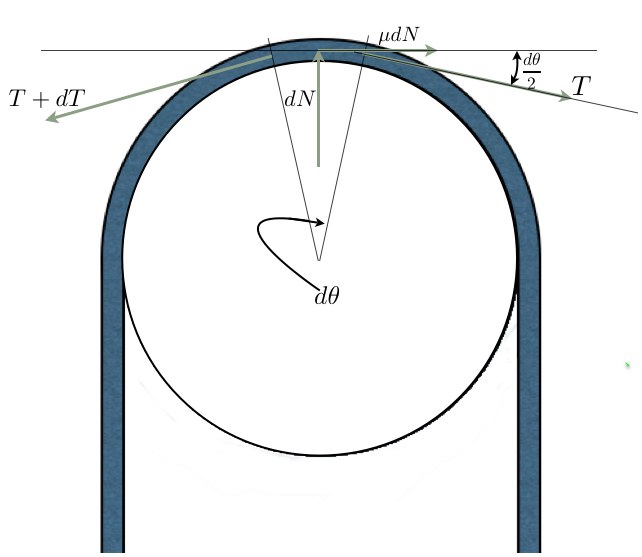
When we have a longer section of rope around a capstan, the tension changes with every length element rubbing against the capstan. The change in tension עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): dT , actually happens with every change in angle, which we call עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): d\alpha . We can call the normal force for every rope element עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): dN . The total friction is a summation (or integration) of the changes in tension over all the rope elements touching the capstan.
In a constant, steady state, the sum of forces vanishes, that is also specifically true for the forces in the עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): x direction.
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \Sigma F_x=0\,\!
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): T\cos\frac{d\theta}{2}+\mu(dN)-(T+dT)\cos\frac{d\theta}{2}=0
since עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): d\theta is very small, and its cosine is very close to one, the expression can be reduced to:
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \mu(dN)=dT\,\!
Similarly, the forces in the עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): y direction cancel each other and from the constraint עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \Sigma F_y=0\,\! , we get:
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): dN-(T+dT)\sin\frac{d\theta}{2}-T\sin\frac{d\theta}{2}=0
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): dN=2T\sin\frac{d\theta}{2}+dT\sin\frac{d\theta}{2}=0
Since a sine of a small number equals that number itself:
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): dN=2T\frac{d\theta}{2}+\frac{dT d\theta}{2}=0
We can ignore the product of two very small expressions and thus:
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): dN=Td\theta\,\!
If we substitute עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): dN , we have an expression that is independent of the normal forces, and is a differential equation that describes עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): T :
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \frac{dT}{T}=\mu d\theta\,\!
In order to find the difference in rope tension on both sides of the capstan we need to integrate the differences on the total angle in which the rope comes in contact with the capstan:
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \int_{T_1}^{T_2}\frac{dT}{T} = \int_0^\alpha \mu d\theta
After the integration we get:
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \ln\frac{T_1}{T_2} = \mu\alpha
The force we need to pull the rope, עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): T_1 is:
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): T_1=T_2e^{\mu\alpha}\,\!
And the friction force is the difference between the tensions on the opposite sides of the capstan:
עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): F_f=T_2(1-e^{\mu\alpha})\,\!
As a matter of fact, with a capstan with a larger diameter than a critical diameter, the friction is independent of the length of rope wrapped (and so independent of the diameter of the capstan) and is only dependent on the total angle of contact.
Half way through summary
We calculated that the friction of a rope on a capstan is determined by three factors:
- Rope tension.
- The friction coefficient.
- The total angle of contact between the rope and capstan.
The friction is directly proportional to the tension, and exponentially rises with the contact angle and the friction coefficient. If we assume that the friction coefficient is constant, for example, NyLon rope with a typical Aluminum alloy (like A7075, frequently used for climbing gear), we can compare between different devices.
It is important to remember, that the coefficient of friction depends strongly on rope characteristics and condition. For a new rope, the friction coefficient is low, and even more so for wet and muddy ropes. For old, worn and "wooly" ropes, the friction coefficient can be significantly higher.
And one more remark about the total contact angle, or the fraction of a wrap, that the rope does around the capstan. This is, in fact, true for capstans larger than a certain critical diameter. That is, however, a pretty good approximation for "soft" ropes only, for capstans that have larger diameter than the rope (i.e. [[Figure of eight, biners, and other friction devices).
It is different with ATC, Reverso and other belay plates, where the rope goes over thinner edges, which simulate a smaller diameter capstan. In these cases the calculation will be different. The rope is then shapes like an up-side down U. There is a very short section of rope that is pressed onto the device, and on both sides, it almost doesn't touch. If we assume that the rope is rigid enough, the normal force on the short segment that is pressed to the device is approximately twice the tension and the friction is very high.
And last, there is the matter of the angle. We are accustomed to measure angles in degrees. In the formulas here, the angle is in radians. If we intend to calculate and get a numerical value, we need to use radians.
We remind that one radian is the angle where the length of the arc of a circle, equals in length to the radius of the same circle. Since we know that the ration between the radius and the circumference is עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): 2\pi , the total angle for a full circle, 360°, is עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): 2\pi radians, or about 6.28 rads. One rad equals approximately 57.29°.
Examples
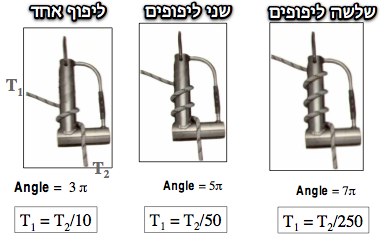
Example 1: A round pole, a tube or a Tuba
This is explained best by the illustration. The change in total contact angle is obvious, and the friction rises accordingly. The numerical ratio between the tensions before and after the friction device were calculated using a friction coefficient of עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \mu = 0.25 .
Each additional wrap of rope around the tube adds 360° or עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): 2\pi radians.
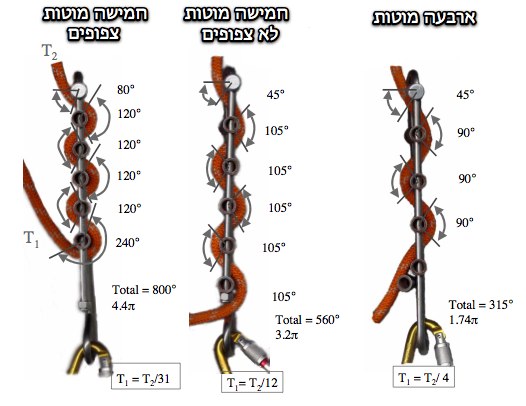
Example 2: A Rack
When using a Rack, there are two main ways of increasing the friction:
The first option is to add bars to the rack. When this is done, the total contact angle increases with a constant amount with each bar added.
The second way to increase friction is by bringing the bars closer together. This makes the rope wrap more around each bar, thus increasing the contact angle for each one of them and, over-whole.
Example 3: Figure of eight
If we look closely at the way the rope passes through a Figure of eight, we can see the difference between the two extreme cases. The first case is the one where it is the easiest to give out rope, and friction is minimal. The total contact angle is then 540° (180°+180°+180°), or עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): 3\pi radians.
In the other extreme case, where there is maximum friction, and the device is "locked", the breaking rope does a 270° (instead of 180° in the previous case) and the total contact angle 630° or עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): 3.5\pi radians.
So, if we use the capstan friction calculation we find that with a Figure of eight, the difference between minimum and maximum friction is only 16.66%. It is a widely accepted that a Figure of eight is not the best device to belay a leader with. It is hard to take in and give out rope fast enough to make it a good choice for that use. On the other hand, the same characteristic makes the Figure of eight a good choice for rappelling. It provides a continuous range of amounts of friction, and even in the "least friction" configuration, it still doesn't let the rope run freely. The transition between the two extreme states is smooth.
Example 4: Sticht plate
Most belay plates based on the Sticht plate have a "breaking area", where the "capstan" over which the rope passes is much thinner than the rope.
Looking at the way the rope passes in a belay plate, we can see a distinct difference between the minimum and maximum friction states. With minimal friction, the rope passes almost only on the biner, and the total contact angle is approximately 180° or עיבוד הנוסחה נכשל (קובץ ההפעלה <code>texvc</code> אינו זמין. נא לעיין ב־math/README כדי להגדירו.): \frac{\pi}{2} radians. With these devices it is very easy to give out and take in rope, much more than with a Figure of eight.
The illustration shows two devices: a Sticht plate and a Tuber.
When "locked", in the breaking position, our calculation is not a good approximation and there is a strong dependence on the radius of the edge of the device, and on the rope knotability.
Example 5: Auto-locking devices
Here we mean mostly single rope auto-locking devices like the Grigri, Stop, ID, but also simpler devices like the Toucan, Reverso, Globus and Gigi when in their auto-lock configuration. When taking in rope (and the device is not locked) the friction can be estimated according to the principles explained above, that is, by estimating the total contact angle of the rope with the capstan. As an example, you can try to compare the friction in a Gigi and in a Grigri.
When locked, the situation is different. Here the capstan theory collapses completely. In these devices the locking increases the friction significantly by pinching the rope in a single, short segment of rope. Therefore, in locked state, the total contact angle is irrelevant, and the locking concentrates on transforming the rope drag to pinching the rope, perpendicular to the rope's motion by using a cam. But that's an altogether different subject.
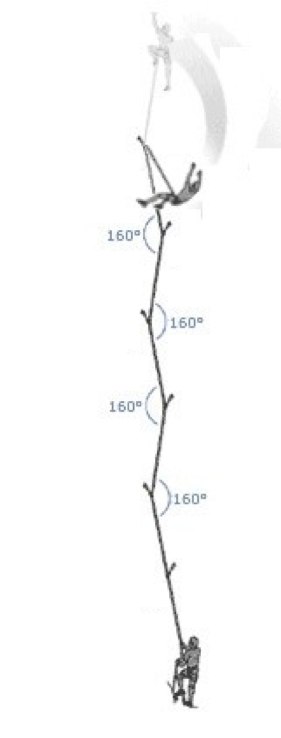
Example 6: Friction in a lead fall
The friction generated by the passage of the rope in the runners' binners during a fall, effectively separates segments of ropes, and causes the tension on each rope segment to be different. We can estimate the difference between the force that the climber feels (Impact force) and the force that the belayer feels. This difference will be the sum of friction of the rope in all the runners. We can calculate that force by summing the angles of contact in all the runners to get the total contact angle (very much like we did for the Rack in Example 2).
It is clear, that if the rope makes a sharp angle passing through a runner, not only that the leader will have more rope drag, but also that in the case of fall, Instead of the fall factor we usually look at, we'll be looking at a fall with an effective fall factor, much greater that the theoretical one, and therefore a higher impact force and a more serious fall.
Links
- The main inspiration for this page
- Another paper, also on friction in different rock types
- and here you can find an analysis of friction forces in different situations: climbingm, rescue, etc.]
Contributions to this page were made by Mica Yaniv and others...
